- ... knowledge)
- It is worth stating, for the record, that the single best reference on this subject is Gunnar Nitsche's doctoral dissertation [131]; I have referred to and borrowed from it quite a bit, and in fact, several topics in this thesis have appeared there, in a somewhat more compact form. Unfortunately, it is only available in German, and this was another reason for attempting a comprehensive review in English.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time
- It should be said, however, that a time-varying acoustic tube is not, strictly speaking, a lossless system--energy is pumped into the system by the variations themselves. While the lossless time-varying concatenated acoustic tube model may be a useful signal processing construct, it can not be said to correspond to the numerical solution of a commonly-known system of PDEs. We will revisit the full time-varying system more rigorously in §6.2.7.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variables
- Another reason for our choice of pressure waves is that when we transfer digital waveguide networks to the electrical framework in Chapter 4, then pressure waves become voltage waves, which are also the signal variables in the wave digital filtering literature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... area
- In order for the network to be synchronic, or realizable as a recursive computer program, all the delay durations must be integer multiples of a common unit delay (the sampling period). Because the physical length of a digital waveguide is directly proportional to the delay (by a factor of
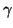 , the wave speed), a synchronic DWN always corresponds to a network of acoustic tubes whose lengths are appropriately quantized.
, the wave speed), a synchronic DWN always corresponds to a network of acoustic tubes whose lengths are appropriately quantized.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... currents
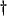
- In the electrical setting, there is of course a dual set of laws describing a series connection, but there is no simple acoustic analogue for such a connection.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... small
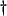
- What we have done, in the jargon of numerical integration methods, is to show the consistency [176] of the waveguide mesh with the two-dimensional wave equation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...waves
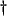
- Though it is perhaps difficult to conceive of wave motion in a lumped system (i.e., one with negligible spatial extent) such as an analog electrical network, it should be mentioned that so-called wave variables may be interpreted as traveling waves in a network whose components are connected by transmission lines of vanishing length [161].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... analysis
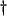
- A good example of such a concern presents itself when we look into spectral analysis of difference schemes in Appendix A. Simulation people are usually interested in the convergence of approximate numerical schemes, in the limit as a grid spacing or time step becomes small; digital filtering people would think of this as matching a digital frequency response to that of the analog response (of the physical system) near the spatial or temporal DC frequency; for musical sound synthesis, however, these grid spacings or time steps are generally fixed (by the sampling rate), so it might be worthwhile to look at a measure of the spectral fit over the entire spectrum.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... free
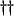
- More generally, network theory treats so-called t-terminal or multi-pole networks [206], for which terminals are not necessarily associated in pairs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrix
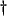
- A linear and time-invariant
 -port need not have an impedance; the ideal transformer, for example, does not. In such cases, a more general ``hybrid'' matrix [12], from which all relevant properties may be deduced, can be defined. We will make special use of hybrid forms in §4.10.
-port need not have an impedance; the ideal transformer, for example, does not. In such cases, a more general ``hybrid'' matrix [12], from which all relevant properties may be deduced, can be defined. We will make special use of hybrid forms in §4.10.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... positive
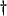
- More generally, we allow these values to be zero as well. In these cases, the inductor and resistor are interpreted as short-circuits, and the capacitor as an open-circuit.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fettweis
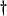
- Fettweis in fact proposes the mapping
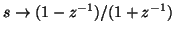 , which is similar to (2.11) except for the factor of
, which is similar to (2.11) except for the factor of  . Although this factor is of little importance in filtering applications, it is necessary here for the interpretation of such mapping as an integration rule. This should become clear in Chapter 3.
. Although this factor is of little importance in filtering applications, it is necessary here for the interpretation of such mapping as an integration rule. This should become clear in Chapter 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...

- Since the two systems are assumed to be the same, modulo a spectral warping, we will not use a special notation to distinguish a discrete variable from a continuous one; the type of variable should be clear from context, and in cases where confusion may arise, we will always explicitly note the argument. In Chapter 4, however, we will use capital letters to distinguish discrete from continuous variables; this notational switch is unfortunate, but is a compromise necessary in order to remain coherent with the different literatures.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... filter
- In this chapter, because all elements are LTI, we could equally well use the symbol
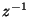 for the unit delay (as is commonplace in the digital filtering literature). In the next chapter, however, when we will be making use of shifts in multiple dimensions for systems which are not, in general, shift-invariant, then frequency domain signal-flow diagrams may only be used in special cases.
for the unit delay (as is commonplace in the digital filtering literature). In the next chapter, however, when we will be making use of shifts in multiple dimensions for systems which are not, in general, shift-invariant, then frequency domain signal-flow diagrams may only be used in special cases.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... adaptors
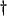
- Referring to Figure 2.10, it is easy to see that the transformer with
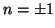 and
and
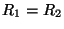 , and the gyrator with
, and the gyrator with
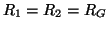 (their most common forms) also are arithmetic-free. Otherwise, a more detailed treatment is required.
(their most common forms) also are arithmetic-free. Otherwise, a more detailed treatment is required.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... type
- It is possible to extend the MDWD approach to cover parabolic systems [176] as well; parabolic systems may not have a bounded propagation velocity, but they can be approximated by hyperbolic systems. This is essentially the path taken by Fettweis in the modeling of the full Navier-Stokes Equations [112] which describe the behavior of a general viscous fluid [49]; we remark that a similar idea, termed ``second-sound theory,'' [26,205] has been used to hyperbolicize parabolic problems (indeed, all time-dependent systems obeying the laws of classical physics must be hyperbolic, even if certain models do not reflect this). Elliptic problems, which typically occur in describing steady state potential distributions in both electrostatics and fluid dynamics can be dealt with using MDWDFs using a relaxation-type approach [47].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrices
- We will always choose
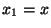 ,
, 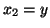 ,
, 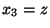 , so the matrices
, so the matrices
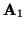 ,
,
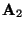 and
and
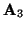 will refer to the matrix coefficients of the partial derivatives in these three directions in (3.1).
will refer to the matrix coefficients of the partial derivatives in these three directions in (3.1).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...mdpassfig
- Adapted from Figure 2 of [85] and Figure 1 of [48].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... case
- We will return to the multidimensional generalization of the unit element in §4.10.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... be

- Given the solution (3.53) to (3.51), it is easy to see that it remains unchanged even if
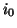 is not differentiable everywhere. In this case,
is not differentiable everywhere. In this case,  must be considered to be a solution to the integral form of (3.51).
must be considered to be a solution to the integral form of (3.51).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... positive
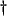
- In fact,
 and
and  should be bounded away from zero, so that the local wave speed (given by
should be bounded away from zero, so that the local wave speed (given by
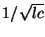 ) remains finite everywhere.
) remains finite everywhere.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... passive
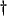
- By concretely passive, we simply mean that all elements in the network should be individually passive. A network (or
 -port [12]) may be abstractly passive, but not concretely passive; the MDKCs shown in Figure 3.11 are of this type.
-port [12]) may be abstractly passive, but not concretely passive; the MDKCs shown in Figure 3.11 are of this type.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1dwdportres
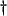
- We have also used the fact that because this system is linear and time-invariant (though not shift-invariant), time-shifting operators such as
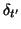 commute with purely spatially-varying quantities such as
commute with purely spatially-varying quantities such as 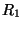 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... limit
- Analysis of a numerical method away from its stability limit is useful because it can give some indication of how the scheme will behave in the presence of material variations; if the system does exhibit such variations, then, locally speaking, we will necessarily be operating away from this limit in at least part of the problem domain.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... system
- We would like to note here that the eigenvectors of the scattering matrix will give extremal values for the quantity
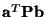 for an
for an  -port with
-port with  -vector input waves
-vector input waves 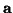 and output waves
and output waves 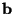 and a diagonal weighting matrix
and a diagonal weighting matrix 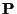 containing port conductances. This quantity, at least for some simple lumped systems, can be identified with what is called as the Lagrangian [190]. Many physics problems (indeed, all the systems treated in this thesis) can be recast as variational problems involving finding an extreme value of the Lagrangian integrated over all possible system states. Though we have not worked out all the details in the distributed case, it would appear that the alignment of the discrete system with an eigenvector of the scattering matrix is the scheme's ``attempt'' to conform to Lagrangian mechanics (which is to be expected). This is interesting for two reasons; first, the wave digital Lagrangian could form the basis for a new set of quantization rules, which, in addition to (or perhaps instead of) ensuring passivity, nudge the system toward a preferred state. Second, the variational or Lagrangian formulation of a physics problem is a necessary first step in developing what are known as finite element methods (FEM) [95]; these methods are not restricted to operating on regular grids, as MDWD methods are. Could MDWD networks operating on unstructured grids be arrived at through such a formulation? This is, admittedly, a very vague notion.
containing port conductances. This quantity, at least for some simple lumped systems, can be identified with what is called as the Lagrangian [190]. Many physics problems (indeed, all the systems treated in this thesis) can be recast as variational problems involving finding an extreme value of the Lagrangian integrated over all possible system states. Though we have not worked out all the details in the distributed case, it would appear that the alignment of the discrete system with an eigenvector of the scattering matrix is the scheme's ``attempt'' to conform to Lagrangian mechanics (which is to be expected). This is interesting for two reasons; first, the wave digital Lagrangian could form the basis for a new set of quantization rules, which, in addition to (or perhaps instead of) ensuring passivity, nudge the system toward a preferred state. Second, the variational or Lagrangian formulation of a physics problem is a necessary first step in developing what are known as finite element methods (FEM) [95]; these methods are not restricted to operating on regular grids, as MDWD methods are. Could MDWD networks operating on unstructured grids be arrived at through such a formulation? This is, admittedly, a very vague notion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...antisymmetrically
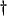
- Recall from §3.2 that the term ``symmetric hyperbolic'' does not refer to the coefficient of the constant-proportional term
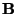 , which is not constrained to be of any particular form.
, which is not constrained to be of any particular form.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... second-order
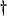
- We remark here that this restriction may be fundamental. It should be recalled that MD systems are passive with respect to the time coordinate--coordinate transformations are simply a means of distributing this passivity property among all the independent variables of the problem. It is well-known [65] that lumped passive systems of first-order can be approximated by passive numerical methods which are at best second-order accurate. This restriction would appear to carry over in MD, though we have not attempted to prove this. Passivity does not hold, however, with respect to the spatial coordinates, and it may be this distinction which we are able to exploit in this section.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... respectively
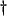
- We have chosen here to break with the notational tradition in [167], in which the superscripts are reversed. We choose the above notation so that signal nomenclature in a waveguide network is well-defined. That is, a signal leaving a bidirectional delay line, and a signal entering a scattering junction (to which each end of the waveguide will ultimately be connected) are both superscripted by a +. This will simplify the derivation of difference schemes later in this chapter. The other indexing method is more useful from the point of view of a unified treatment of both scattering junctions and bidirectional delay lines as digital n-port devices (where we would want + and
 to denote incoming and outgoing signals, respectively, for any
to denote incoming and outgoing signals, respectively, for any  -port).
-port).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... filters
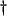
- This is often essential, because working at the audio sampling rate often forces a large grid spacing. In an acoustic tube, for example, the wave speed is
 m/s. At the audio sampling rate we will have a waveguide delay of
m/s. At the audio sampling rate we will have a waveguide delay of
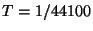 s, which implies a waveguide length of
s, which implies a waveguide length of
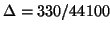 m = 0.75 cm. For a woodwind instrument, this distance is on the order of the tone hole separation distance, and will thus be far too crude for good physical modelling.
m = 0.75 cm. For a woodwind instrument, this distance is on the order of the tone hole separation distance, and will thus be far too crude for good physical modelling.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... alone
- Even if
 and
and  are functions of
are functions of  , it is still possible to reduce system (4.17) to a second order equation in the voltage alone, but it does not have the simple form of (4.18).
, it is still possible to reduce system (4.17) to a second order equation in the voltage alone, but it does not have the simple form of (4.18).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...

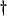
- In any case where the time index
 is omitted, we mean for the statement to hold at any time step.
is omitted, we mean for the statement to hold at any time step.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...

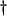
- We take care to distinguish these quantities, which are simply values of the continuous functions
 and
and  from the indeterminate quantities
from the indeterminate quantities
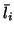 and
and
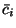 defined in (4.21).
defined in (4.21).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... well
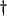
- In fact, we are being somewhat cavalier here (as we will be again when we look at the tetrahedral mesh in §4.7), because the updating is not the same at every junction. We will deal with this aspect in full detail in Appendix A.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form
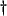
- It is in the same form except for the scaling parameter
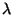 which was introduced so as to allow a different grid spacing in the two radial coordinate directions; such a scaling parameter may be used here to exactly the same effect.
which was introduced so as to allow a different grid spacing in the two radial coordinate directions; such a scaling parameter may be used here to exactly the same effect.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... way
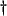
- Fettweis has already defined a multidimensional unit element in [44], but in that case, shifts in a single direction were used in both delay paths; the multidimensional unit element defined here can be thought of as a simple generalization of this structure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form
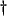
- We leave out the supplemental relations
where 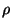 is the charge density. These can be viewed as extra restrictions on the allowed solutions to (4.110).
is the charge density. These can be viewed as extra restrictions on the allowed solutions to (4.110).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... diagonal

- It is possible to write a symmetric hyperbolic form of Mindlin's system for which the
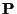 matrix is diagonal by introducing the variables
matrix is diagonal by introducing the variables
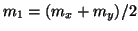 and
and
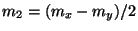 . Though the resulting MDKC will be simpler, boundary conditions become over-determined and difficult to set properly, because
. Though the resulting MDKC will be simpler, boundary conditions become over-determined and difficult to set properly, because
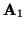 and
and
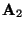 are consequently less sparse (implying greater network connectivity). The form described by the matrices in (5.33) is more fundamental in this respect.
are consequently less sparse (implying greater network connectivity). The form described by the matrices in (5.33) is more fundamental in this respect.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... circuit
- In keeping with the notation of Chapter 4, we have appended a ``
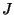 '' to the subscript of any grid function, to indicate that it is to be calculated as a junction current or voltage.
'' to the subscript of any grid function, to indicate that it is to be calculated as a junction current or voltage.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variables
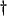
- The reason for the unusual numbering of these variables will be made clear in the next section.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elements
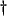
- Recall that a reciprocal circuit element is one whose impedance matrix (more generally, its hybrid matrix) is Hermitian.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... years

- Spectral, or Von Neumann analysis [176], which we will discuss in Appendix A, and the energy method [82] are two branches of this theory which have great bearing on the subject of this thesis. We have not, unfortunately, had the time to fully explore the latter direction, which will surely be more than a little enlightening.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time
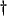
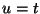 , for instance, satisfies (A.1).
, for instance, satisfies (A.1).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equation
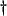
- Regrettably, a full discussion of consistency of difference schemes would take us too far afield, and we refer to [176] for a full exposition. The idea, grossly speaking, is that for a stable difference scheme, consistency is our guarantee that the numerical solution to the difference scheme converges to the solution of the continuous model problem as the grid spacing and time step are decreased. It is usually checked via a Taylor expansion of the difference scheme.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frequencies
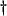
- As an example of such growth at the spatial DC frequency, consider initializing the scheme (A.14) using
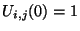 for
for 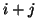 even and
even and
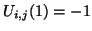 for
for 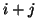 odd. Then we will have
odd. Then we will have
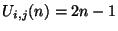 , for
, for 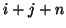 even. It is simple to show that a waveguide implementation does not allow us to choose bounded wave variable initial conditions which yield these values for
even. It is simple to show that a waveguide implementation does not allow us to choose bounded wave variable initial conditions which yield these values for
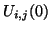 and
and
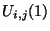 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... open
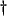
- We consider this to be the single most important issue raised in this thesis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... differentiable
- This is an assumption made by Fettweis et al. in all of their fluid dynamics work, and is not entirely justified, especially if discontinuities (shocks) are to be modeled. Even in the simple model of Burger's equation, these shocks can develop [82]. Over regions of continuity in the problem, these numerical methods will give the correct solution, but shock velocities, should they develop, may not be correct for this reason.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elements
- We note, however, that Fries [70] has obtained an MDKC directly from these conservation laws, though certain extra parameters must be introduced in order to control stability.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.