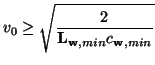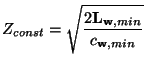Next: Interfaces Between Grids
Up: Digital Waveguide Networks
Previous: The (3+1)D Wave Equation
The Waveguide Mesh in General Curvilinear Coordinates
A generalization of the waveguide mesh to arbitrary curvilinear coordinates is useful in that it becomes possible to model boundary conditions which may not be simply aligned with a rectilinear grid. The resulting structure is quite similar to the interleaved forms discussed earlier, and for this reason we will give only a brief description of the coordinate transformation procedure. Consider the following system:
 |
(4.113a) |
Here we may assume any number  of physical spatial coordinates
of physical spatial coordinates
![$ {\bf x} = [x_{1}, \hdots, x_{k}]^{T}$](img1883.png) , so that
, so that
![$ \nabla_{{\bf x}} = \frac{\partial}{\partial {\bf x}} = [\frac{\partial}{\partial x_{1}},\hdots, \frac{\partial}{\partial x_{k}}]^{T}$](img1884.png) .
.
 and
and
 are both assumed to be
are both assumed to be  -dimensional column vectors.
-dimensional column vectors.
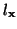 ,
,
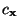 ,
,
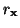 and
and
 are all positive functions of
are all positive functions of 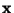 (
(
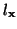 and
and
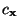 are strictly positive), and
are strictly positive), and
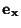 and
and
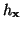 are the source terms. If
are the source terms. If  is 1 or 2, then we have the transmission line or parallel-plate transmission line system respectively, and if
is 1 or 2, then we have the transmission line or parallel-plate transmission line system respectively, and if 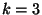 , we have the system describing linear acoustic phenomena (assuming that the material parameters are constant).
, we have the system describing linear acoustic phenomena (assuming that the material parameters are constant).
Consider the mapping
where
![$ {\bf w} = [w_{1}, \hdots, w_{k}]^{T}$](img1896.png) are the transformed coordinates. A rectilinear grid in the
are the transformed coordinates. A rectilinear grid in the 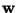 coordinates can be mapped to a curvilinear grid in the physical
coordinates can be mapped to a curvilinear grid in the physical 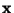 coordinates. We can then define the
coordinates. We can then define the 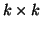 matrix of partial derivatives
matrix of partial derivatives 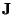 by
by
where
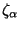 is the
is the 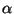 th component of
th component of 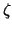 . We assume
. We assume 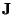 to be nonsingular everywhere in the problem domain (though this assumption may be relaxed as will mention later in this section) . Defining the differential operator
to be nonsingular everywhere in the problem domain (though this assumption may be relaxed as will mention later in this section) . Defining the differential operator
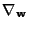 by
by
![$ \nabla_{{\bf w}} = \frac{\partial}{\partial {\bf w}} = [\frac{\partial}{\partial w_{1}},\hdots, \frac{\partial}{\partial w_{k}}]^{T}$](img1903.png) , it then follows [69] that
, it then follows [69] that
for any 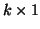 column vector
column vector 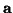 . Here,
. Here, 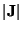 is the so-called Jacobian determinant [172]. Using these relationships, the system (4.97) may be rewritten as
is the so-called Jacobian determinant [172]. Using these relationships, the system (4.97) may be rewritten as
or
 |
(4.114a) |
where
and
System (4.98) is similar to (4.97), except that we now have ``vector'' inductance and resistance coefficients (note that both
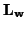 and
and
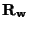 are positive definite matrices, if
are positive definite matrices, if 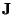 is non-singular). In particular, it is still symmetric hyperbolic (see §3.2), so we may expect that it is possible to derive a waveguide structure.
is non-singular). In particular, it is still symmetric hyperbolic (see §3.2), so we may expect that it is possible to derive a waveguide structure.
Consider now the transformed system (4.98) in (2+1)D. If
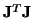 is diagonal, then
is diagonal, then
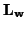 and
and
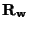 will be as well; in this case, system (4.98) is in the same form
will be as well; in this case, system (4.98) is in the same form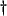 as the parallel-plate system in radial coordinates (4.82), so we need not discuss this case further here. Indeed, the radial system is a special case of (4.98) with
as the parallel-plate system in radial coordinates (4.82), so we need not discuss this case further here. Indeed, the radial system is a special case of (4.98) with
![$ {\bf w} = [\rho, \theta]^{T}$](img1929.png) and
and
On the other hand, if
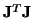 is not diagonal (so that we are working in non-orthogonal or oblique coordinates), then the situation is more complex. Due to the cross-coupling between the components of
is not diagonal (so that we are working in non-orthogonal or oblique coordinates), then the situation is more complex. Due to the cross-coupling between the components of
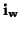 through the matrices
through the matrices
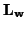 and
and
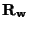 , it will no longer be possible to stagger all the components of the solution; in particular, it will be necessary to use vector scattering junctions. Let us look at the case
, it will no longer be possible to stagger all the components of the solution; in particular, it will be necessary to use vector scattering junctions. Let us look at the case 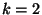 , so that (4.98) are the equations of the parallel-plate system in the curvilinear coordinates
, so that (4.98) are the equations of the parallel-plate system in the curvilinear coordinates 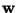 . Furthermore, we will set
. Furthermore, we will set 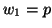 and
and 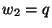 . A centered difference approximation to (4.98), over grid points with coordinates
. A centered difference approximation to (4.98), over grid points with coordinates 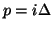 and
and 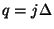 , and at times
, and at times 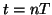 for
for  ,
, 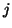 and
and  half-integer is
half-integer is
Here, we have the vector grid function
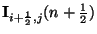 , which is a two-vector with components
, which is a two-vector with components
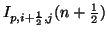 and
and
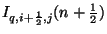 as well as the scalar grid function
as well as the scalar grid function
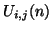 .
.
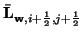 and
and
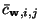 are second-order approximations to
are second-order approximations to
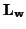 and
and
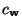 at the indicated grid points. The scheme above has been written so that it is clear that it can operate for
at the indicated grid points. The scheme above has been written so that it is clear that it can operate for  integer, and for
integer, and for  and
and 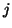 such that
such that 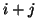 is integer; notice that
is integer; notice that 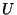 and
and 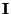 are calculated at alternating time instants and grid locations, but the components of
are calculated at alternating time instants and grid locations, but the components of 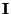 can not, in general, be calculated at separate locations.
can not, in general, be calculated at separate locations. 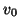 , again, is equal to
, again, is equal to 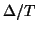 , and (4.99) will be a second-order accurate approximation to (4.98).
, and (4.99) will be a second-order accurate approximation to (4.98).
We will skip the tedious procedure of deriving a waveguide mesh, and simply present the resulting structure in Figure 4.34.
Figure 4.34:
(2+1)D DWN for the parallel-plate system (4.98) in general non-orthogonal curvilinear coordinates.
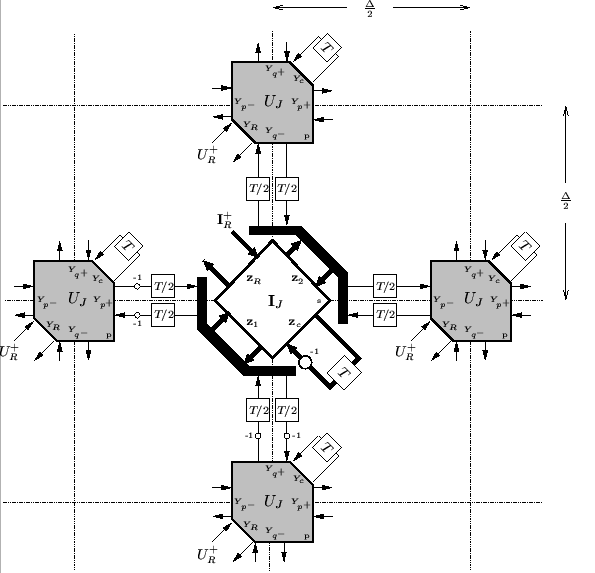 |
Junction vector currents
 are calculated at the series vector scattering junctions; the black bars surrounding this junction in the figure are the splitting elements that were discussed in §4.2.6. Although we have not drawn them in the figure, there will be similar vector junctions at the four grid points neighboring any of the parallel junctions where the voltages
are calculated at the series vector scattering junctions; the black bars surrounding this junction in the figure are the splitting elements that were discussed in §4.2.6. Although we have not drawn them in the figure, there will be similar vector junctions at the four grid points neighboring any of the parallel junctions where the voltages 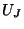 are calculated. This vector junction has four
are calculated. This vector junction has four  matrix impedances associated with it:
matrix impedances associated with it:
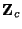 , the self-loop impedance,
, the self-loop impedance,
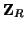 , the loss/source impedance, and
, the loss/source impedance, and
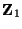 and
and
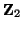 , which are constrained (see §4.2.6) to be
, which are constrained (see §4.2.6) to be
 |
(4.116) |
The junction impedance
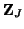 is defined to be the sum of these four matrices. The admittances at the parallel junctions are defined in a manner similar to those of the DWN in rectilinear coordinates. Also, we have the source voltage waves
is defined to be the sum of these four matrices. The admittances at the parallel junctions are defined in a manner similar to those of the DWN in rectilinear coordinates. Also, we have the source voltage waves
 at the parallel junctions and vector source current waves
at the parallel junctions and vector source current waves
 at the series junctions.
at the series junctions.
This DWN can be identified with the difference system (4.99) if we set
at the grid points for which such quantities are defined.
There are, of course, various realizations, depending on how the self-loop and connecting immittances are chosen. First, note that because
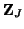 is not diagonal, it will not be possible to distribute it equally among the two connecting impedances
is not diagonal, it will not be possible to distribute it equally among the two connecting impedances
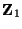 and
and
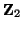 , which are constrained to be diagonal from (4.100). Thus a type II (current-centered) realization analogous to that which was discussed in the case of the rectilinear mesh will not be possible, even in the absence of losses and sources. A type I realization is certainly possible, but for brevity sake, we will only provide the settings for the type III DWN. Here all the connecting impedances are all set to be some constant value
, which are constrained to be diagonal from (4.100). Thus a type II (current-centered) realization analogous to that which was discussed in the case of the rectilinear mesh will not be possible, even in the absence of losses and sources. A type I realization is certainly possible, but for brevity sake, we will only provide the settings for the type III DWN. Here all the connecting impedances are all set to be some constant value 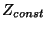 . This then implies that
. This then implies that
where
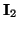 is the
is the  identity matrix. Requiring the positivity of
identity matrix. Requiring the positivity of 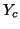 and the positive definiteness of
and the positive definiteness of
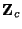 gives the constraint
gives the constraint
for
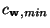 the minimum of
the minimum of
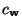 over parallel junction locations and
over parallel junction locations and
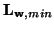 the minimum of the eigenvalues of
the minimum of the eigenvalues of
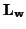 over series junction locations, and where we have made the choice
over series junction locations, and where we have made the choice
In general, this bound will depend on the choice of coordinates.
FDTD in general curvilinear coordinates has developed in a similar way; most formulations are slightly different in that they are based on a tensor density formulation [91,209] and employ a double set of variables (covariant and contravariant) in the non-orthogonal case; differencing involves interleaving these two sets of components at alternating time steps. They have also been used as a starting point for developing FDTD methods in ``local'' coordinates defined with respect to an automatically generated grid [72,73]. Curvilinear coordinate systems have been touched upon in the MDWD framework as well; An approach similar to the above is discussed in [69], and a tensor density formulation is given in [131].



Next: Interfaces Between Grids
Up: Digital Waveguide Networks
Previous: The (3+1)D Wave Equation
Stefan Bilbao
2002-01-22
![$\displaystyle [{\bf J}_{\alpha,\beta}] = \frac{\partial\zeta_{\alpha}}{\partial w_{\beta}}\hspace{0.5in}\alpha,\,\beta = 1,\hdots,k$](img1899.png)
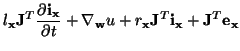
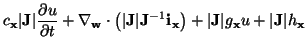
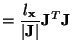
![]() is diagonal, then
is diagonal, then
![]() and
and
![]() will be as well; in this case, system (4.98) is in the same form
will be as well; in this case, system (4.98) is in the same form![]() as the parallel-plate system in radial coordinates (4.82), so we need not discuss this case further here. Indeed, the radial system is a special case of (4.98) with
as the parallel-plate system in radial coordinates (4.82), so we need not discuss this case further here. Indeed, the radial system is a special case of (4.98) with
![]() and
and
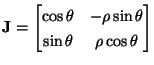
![]() is not diagonal (so that we are working in non-orthogonal or oblique coordinates), then the situation is more complex. Due to the cross-coupling between the components of
is not diagonal (so that we are working in non-orthogonal or oblique coordinates), then the situation is more complex. Due to the cross-coupling between the components of
![]() through the matrices
through the matrices
![]() and
and
![]() , it will no longer be possible to stagger all the components of the solution; in particular, it will be necessary to use vector scattering junctions. Let us look at the case
, it will no longer be possible to stagger all the components of the solution; in particular, it will be necessary to use vector scattering junctions. Let us look at the case ![]() , so that (4.98) are the equations of the parallel-plate system in the curvilinear coordinates
, so that (4.98) are the equations of the parallel-plate system in the curvilinear coordinates ![]() . Furthermore, we will set
. Furthermore, we will set ![]() and
and ![]() . A centered difference approximation to (4.98), over grid points with coordinates
. A centered difference approximation to (4.98), over grid points with coordinates ![]() and
and ![]() , and at times
, and at times ![]() for
for ![]() ,
, ![]() and
and ![]() half-integer is
half-integer is

![]() is not diagonal, it will not be possible to distribute it equally among the two connecting impedances
is not diagonal, it will not be possible to distribute it equally among the two connecting impedances
![]() and
and
![]() , which are constrained to be diagonal from (4.100). Thus a type II (current-centered) realization analogous to that which was discussed in the case of the rectilinear mesh will not be possible, even in the absence of losses and sources. A type I realization is certainly possible, but for brevity sake, we will only provide the settings for the type III DWN. Here all the connecting impedances are all set to be some constant value
, which are constrained to be diagonal from (4.100). Thus a type II (current-centered) realization analogous to that which was discussed in the case of the rectilinear mesh will not be possible, even in the absence of losses and sources. A type I realization is certainly possible, but for brevity sake, we will only provide the settings for the type III DWN. Here all the connecting impedances are all set to be some constant value ![]() . This then implies that
. This then implies that