


Next: Doubled Grid Density Across
Up: Digital Waveguide Networks
Previous: The Waveguide Mesh in
Interfaces Between Grids
In (2+1)D, we have looked so far at numerically solving the parallel-plate transmission line system over regular grids--that is to say, grids whose points can be indexed with respect to some regular coordinate system. We now examine ways of connecting grids of different types, and in particular grids of differing densities of points. The ability to decompose a domain into regions of different grid point densities is especially useful when dealing with boundaries and irregular features (i.e., variations in material parameters) throughout the problem domain; we may use a fine grid to calculate the solution to a problem in such regions, and then a coarse grid everywhere else. The problem, then, is in connecting the various subgrids so that consistency of a numerical method with the original set of equations to be solved can be maintained at the boundaries between the regions. The use of multi-grid techniques in numerical integration had developed into a very large field recently, and we can not hope to summarize the many developments that have taken place, nor even the basic theory. Unfortunately, there is not as yet a single good basic reference; we refer the reader to [140] for an general introduction. Multi-grid methods have been used in the TLM framework, but the structures there employed are somewhat different. In particular, the methods proposed in [88] and [87] (and reviewed in [29]) do not, in general, enforce passivity at an interface between a coarse and fine grid, though they are capable of operating using different time steps in the coarse and fine meshes. The method of [207] is perhaps closer in spirit to that presented here, in that the time step is everywhere the same, but in that case, certain a priori assumptions are made about the fields at the interface.
We will show that it is in fact possible to devise passive connections between waveguide networks (themselves generally passive, unless sources are present) which operate on different types of grids, so that passivity can be maintained in a global sense--there is, as before, an energy measure for the network which can be expressed as a weighted sum of the squares of the wave variables in the network. In this section, we will look in particular at the lossless, source-free parallel-plate equations in (2+1)D (system (4.58) with 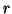 =
= 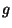 =
= 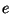 =
= 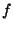 =
= 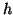 = 0 everywhere). Furthermore, for simplicity, we will confine our attention to waveguide networks of type II as described in §4.4; it will be recalled that for type II networks, when
= 0 everywhere). Furthermore, for simplicity, we will confine our attention to waveguide networks of type II as described in §4.4; it will be recalled that for type II networks, when 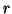 =
= 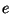 =
= 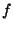 = 0, there is no scattering at the series junctions, and we need only calculate voltages at the parallel junctions.
= 0, there is no scattering at the series junctions, and we need only calculate voltages at the parallel junctions.  and
and  will still be allowed to vary over the problem domain. (It may be possible to extend the multi-grid methods to be described here to the full lossy system including sources, but we will not pursue this direction here.)
will still be allowed to vary over the problem domain. (It may be possible to extend the multi-grid methods to be described here to the full lossy system including sources, but we will not pursue this direction here.)
Subsections



Next: Doubled Grid Density Across
Up: Digital Waveguide Networks
Previous: The Waveguide Mesh in
Stefan Bilbao
2002-01-22
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() = 0 everywhere). Furthermore, for simplicity, we will confine our attention to waveguide networks of type II as described in §4.4; it will be recalled that for type II networks, when
= 0 everywhere). Furthermore, for simplicity, we will confine our attention to waveguide networks of type II as described in §4.4; it will be recalled that for type II networks, when ![]() =
= ![]() =
= ![]() = 0, there is no scattering at the series junctions, and we need only calculate voltages at the parallel junctions.
= 0, there is no scattering at the series junctions, and we need only calculate voltages at the parallel junctions. ![]() and
and ![]() will still be allowed to vary over the problem domain. (It may be possible to extend the multi-grid methods to be described here to the full lossy system including sources, but we will not pursue this direction here.)
will still be allowed to vary over the problem domain. (It may be possible to extend the multi-grid methods to be described here to the full lossy system including sources, but we will not pursue this direction here.)