Progressive Grid Density Doubling

The delays in the bidirectional delay lines of the combined coarse/fine grid of the previous section were everywhere identical. In this section, we will look at networks for which this is not true--all delay line lengths, though, will be multiples of a common smallest unit delay, in order that the network remain synchronous [46]. It should be said, though, that even in a portion of the network where the delay line lengths are longer than a single sample delay, we will still be scattering at the rate of the smallest delay line length in the system as a whole. We will, however, be performing scattering operations at fewer points in the coarse regions. We will call such structures (for lack of a better word) multi-rate, though it should be understood that such networks are not multi-rate in the sense of [193] (see above comment). Specifically, we will focus on the use of such structures in order to extend the grid refinement technique introduced in the previous section.

Figure 4.38: (a) Mesh $I$, with grid spacing $\Delta$, is adjoined to a doubled density mesh $II$, which is in turn adjoined to a quadrupled density mesh $III$, with grid spacing $\frac{\Delta}{2}$ and a halved waveguide delay. (b) A scattering junction at a point $B$ on the boundary between layers $II$ and $III$.

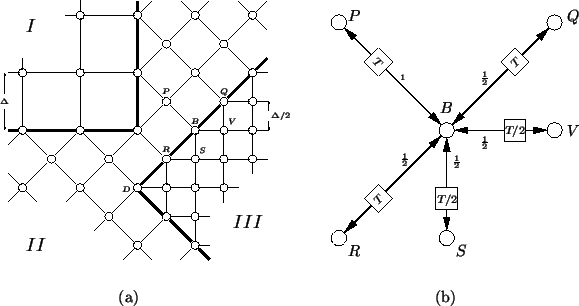
Consider the grid arrangement of Figure 4.38(a). The interface between region $I$ and region $II$ was discussed in the previous section; in that case, we assumed the waveguide delays to be identical everywhere in regions $I$ and $II$, including the boundary. We can, of course, apply the same idea again in order to introduce a grid of quadrupled point density, by adjoining it to region $II$. In this case, however, we would like to take advantage of the fact that waveguide lengths in region $III$ are half those of region $I$; it is more natural, then, to use a delay of half that of region $I$ throughout the interior of region $III$. Waveguides which run along the boundary will still operate at the rate of regions $I$ and $II$, as will the self-loop (of admittance $Y_{c}$, not shown). A scattering junction at a typical point $B$ on the boundary between regions $II$ and $III$ is shown in Figure 4.38(b). Here, we have abbreviated the depiction of a bidirectional delay line to a single double-headed arrow, and have omitted the self-loop (which contains a full unit delay). Note in particular that for such a boundary junction, the delays of the connecting waveguides are now not all identical. As might be expected, the difference scheme relating the junction voltage at such a point to those of its neighbors is no longer a simple two-step difference method, but a four-step scheme, where each time step is now $\frac{T}{2}$; a full derivation of this difference scheme is very lengthy but rewarding, in the sense that it becomes clear why it takes four steps for the wave variables to fully ``recombine'' into junction voltages. We will, however, only present the resulting difference equation for a boundary junction at location $B$ as in Figure 4.38(b). Here the junction voltage will be $U_{J,B}$, and the junction voltages at the neighboring points are, referring to Figure 4.38(b), $U_{J,P},\hdots, U_{J,V}$. The admittances of the connecting waveguides will be called $Y_{PB},\hdots, Y_{VB}$, the self-loop admittance $Y_{c,B}$ and the junction admittance at point $B$ is defined as

$$Y_{J,B} = Y_{PB}+Y_{QB}+Y_{RB}+Y_{SB}+Y_{VB}+Y_{c,B}$$

We have

$$\frac{Y_{J,B}}{2}U_{J,B}(n+1) = \hspace{0.05in}Y_{VB}U_{J,V}(n+{\textstyle \frac{1}{2}})+Y_{SB}U_{J,S}(n+{\textstyle \frac{1}{2}})\notag$$

$$+ Y_{QB}U_{J,Q}(n) + Y_{PB}U_{J,P}(n)+Y_{RB}U_{J,R}(n)\notag$$

$$+ \left(Y_{c,B}-Y_{SB}-Y_{VB}\right)U_{J,B}(n)\notag$$

$$+ Y_{VB}U_{J,V}(n-{\textstyle \frac{1}{2}})+Y_{SB}U_{J,S}(n-{\textstyle \frac{1}{2}})\notag$$

$$- \frac{Y_{J,B}}{2}U_{J,B}(n-1)$$

A Taylor series expansion allows us to set the admittances of the waveguides to be

$$Y_{PB} = \frac{1}{v_{0}l_{PB}}\hspace{0.2in}Y_{QB} = \frac{1}{2v_{0}l_{QB}} \hspace{0.2in}Y_{RB} = \frac{1}{2v_{0}l_{RB}}\notag$$

$$Y_{SB} = \frac{1}{2v_{0}l_{SB}}\hspace{0.2in}Y_{VB} = \frac{1}{2v_{0}l_{VB}}$$

where $l_{XY}$ is the material inductance at the point midway between points $X$ and $Y$. Note in particular that the setting of $Y_{PB}$ coincides with an interior point setting of a connecting waveguide admittance in the interior of region $II$, from (4.64) and (4.65). These relative strengths of the connecting waveguide admittances are indicated by adjacent small numbers in Figure 4.38(b).

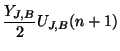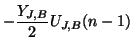Because we now have a four-step scheme, the determination of $Y_{c,B}$ is no longer as simple as in the two-step case, but it can be found, nevertheless, to be

$$Y_{c,B} =\hspace{0.1in} \frac{v_{0}}{8}\left(2c_{PB}+c_{QB}+c_{RB}+c_{SB}+c_{VB}\right)\notag$$

$$- \frac{5}{12v_{0}}\left(\frac{2}{l_{PB}}+\frac{1}{l_{QB}}+\frac{1}{l_{RB}}+\frac{1}{l_{SB}}+\frac{1}{l_{VB}}\right)$$

where $c_{XY}$ signifies a waveguide midpoint evaluation of $c$ between any points $X$ and $Y$.

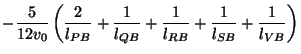The positivity requirement yields the bound

$$v_{0}\geq \max_{\begin{minipage}[t]{1.0in}\begin{center}\tiny {II/III boundary waveguide midpoints}\end{center}\end{minipage}}\sqrt{\frac{10}{3lc}}$$

Corners present essentially the same problems as before, and we will not discuss them further, other than to repeat that, given the settings derived above for the waveguide admittances at the $II$/$III$ boundary, which determine completely the scattering behavior at the corners (an example of which is point $D$ in Figure 4.38(a)), the mesh will not be consistent with the parallel-plate system at these points.