


Next: Extension to (2+1)D
Up: Multidimensional Wave Digital Filters
Previous: Note on Perfectly Matched
Balanced Forms
Consider again the (1+1)D transmission line, with spatially-varying coefficients. It has been noted in the past [130,131] that the restriction on the time step, namely
with
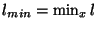 and
and
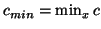 is rather unsatisfying; the local group velocity at any point in our domain is given by
is rather unsatisfying; the local group velocity at any point in our domain is given by
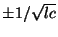 , so we would hope that a more physically meaningful bound such as
, so we would hope that a more physically meaningful bound such as
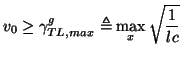 |
(3.93) |
(which is obtained in using, for example, digital waveguide networks, which will be discussed in Chapter 4) could be attainable. Depending on the variation in  and
and  , the new bound can allow a substantially larger time step. We will show that this is in fact possible via a MDWD approach.
, the new bound can allow a substantially larger time step. We will show that this is in fact possible via a MDWD approach.
The transmission line equations given in (3.56) can be transformed in the following way: first introduce new dependent variables
where 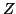 , the local line impedance is defined by
, the local line impedance is defined by
Such a transformation in fact changes to variables which both have units of root power. After a few elementary manipulations (namely scaling (3.56a) by
 and (3.56b) by
and (3.56b) by 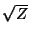 ), we have
), we have
 |
(3.94a) |
System (3.91) is still symmetric hyperbolic; referring to the general system from (3.1), for
![$ {\bf w} = [\tilde{i}_{1}, \tilde{i}_{2}]^{T}$](img1036.png) , we now have
, we now have
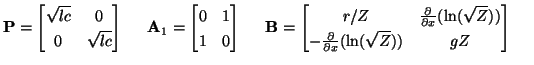 |
(3.95) |
Note that because 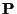 is now a multiple of the identity matrix, there is near complete symmetry between the variables
is now a multiple of the identity matrix, there is near complete symmetry between the variables
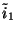 and
and
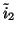 . We use the term ``balanced'' to describe such a system. Note also that new off-diagonal terms have appeared in
. We use the term ``balanced'' to describe such a system. Note also that new off-diagonal terms have appeared in 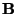 (compare (3.92) with (3.57)), but they appear antisymmetrically
(compare (3.92) with (3.57)), but they appear antisymmetrically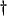 , and thus do not give rise to loss--in other words these terms do not appear in
, and thus do not give rise to loss--in other words these terms do not appear in
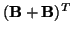 , which determines the growth or decay of the solution, as per (3.5). In fact, these off-diagonal terms yield a lossless (but non-reciprocal) gyrator in the circuit setting.
, which determines the growth or decay of the solution, as per (3.5). In fact, these off-diagonal terms yield a lossless (but non-reciprocal) gyrator in the circuit setting.
In terms of the coordinates defined by (3.18), we can then rewrite (3.91) as
where
(which should be compared with (3.63), for the standard form), and
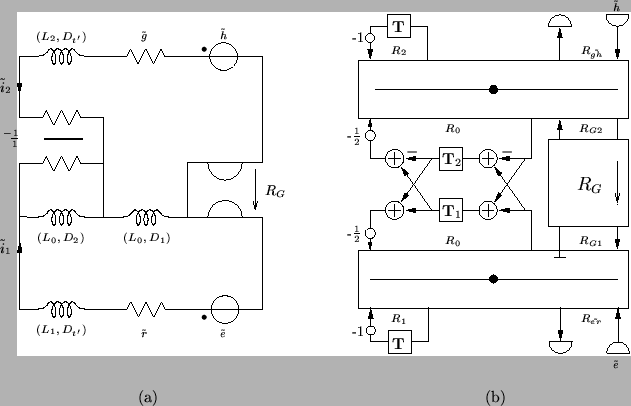
As mentioned previously, in a MDKC setting, the terms with coefficient 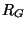 can be treated as a gyrator. The network and its wave digital counterpart are shown in Figure 3.23. The port resistances are given by
can be treated as a gyrator. The network and its wave digital counterpart are shown in Figure 3.23. The port resistances are given by
Figure 3.23: (a) Balanced MD-passive network for the (1+1)D transmission line equations and (b) its associated MDWD network.
 |
In order to accommodate the gyrator, we have been forced, in order to avoid delay-free loops, to set one of the ports to which it is connected to be reflection-free (see §2.3.5). In (1+1)D, we can choose either of these ports, but picking the bottom port in Figure 3.23(b) allows us to extend the idea to (2+1)D easily. This port resistance is then constrained to be
We have two simplifying choices for 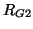 ; either we can choose it to be reflection-free as well, so that we will have a general gyrator described by (2.25), or we can choose
; either we can choose it to be reflection-free as well, so that we will have a general gyrator described by (2.25), or we can choose
in which case the gyrator equations (2.25) reduce to a pair of throughs, scaled individually by
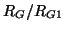 and its inverse; this latter choice may be problematic if
and its inverse; this latter choice may be problematic if 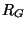 approaches zero, because one of the multipliers becomes unbounded. If
approaches zero, because one of the multipliers becomes unbounded. If 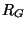 is small over some part of the problem domain, however, it is probably wiser to remove the coupling from the network altogether over these regions (it can be replaced by a simple two-port short-circuit). We have assumed, throughout this development, that
is small over some part of the problem domain, however, it is probably wiser to remove the coupling from the network altogether over these regions (it can be replaced by a simple two-port short-circuit). We have assumed, throughout this development, that 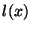 and
and 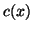 (or rather, the local characteristic line impedance
(or rather, the local characteristic line impedance
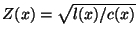 ) are differentiable. An offset-sampled version of this network is also possible, if we halve the port resistances
) are differentiable. An offset-sampled version of this network is also possible, if we halve the port resistances 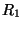 and
and 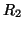 and double the delays at the same ports.
and double the delays at the same ports.
The stability bound, from a requirement on the positivity of 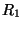 and
and 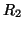 will be exactly (3.90). In an implementation, there will be of course the slight additional costs due to the extra gyrator and the rescaling of the new dependent variables
will be exactly (3.90). In an implementation, there will be of course the slight additional costs due to the extra gyrator and the rescaling of the new dependent variables
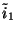 and
and
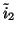 at every time step in order to obtain
at every time step in order to obtain  and
and 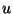 . We note that this scaling can be fully incorporated into the MDKC by treating the scaling coefficients as transformer turns-ratios, though there is no advantage in doing so (other than putting one's mind at ease regarding whether such a scaling is a passive operation).
. We note that this scaling can be fully incorporated into the MDKC by treating the scaling coefficients as transformer turns-ratios, though there is no advantage in doing so (other than putting one's mind at ease regarding whether such a scaling is a passive operation).
We will examine how this same technique can be applied to more complex systems when we approach the Timoshenko beam equations in §5.2; in that case, the maximum allowable time step can be radically increased for a system with only mild material parameter variation.
Subsections



Next: Extension to (2+1)D
Up: Multidimensional Wave Digital Filters
Previous: Note on Perfectly Matched
Stefan Bilbao
2002-01-22
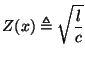
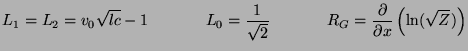
![]() can be treated as a gyrator. The network and its wave digital counterpart are shown in Figure 3.23. The port resistances are given by
can be treated as a gyrator. The network and its wave digital counterpart are shown in Figure 3.23. The port resistances are given by

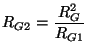
![]() and
and ![]() will be exactly (3.90). In an implementation, there will be of course the slight additional costs due to the extra gyrator and the rescaling of the new dependent variables
will be exactly (3.90). In an implementation, there will be of course the slight additional costs due to the extra gyrator and the rescaling of the new dependent variables
![]() and
and
![]() at every time step in order to obtain
at every time step in order to obtain ![]() and
and ![]() . We note that this scaling can be fully incorporated into the MDKC by treating the scaling coefficients as transformer turns-ratios, though there is no advantage in doing so (other than putting one's mind at ease regarding whether such a scaling is a passive operation).
. We note that this scaling can be fully incorporated into the MDKC by treating the scaling coefficients as transformer turns-ratios, though there is no advantage in doing so (other than putting one's mind at ease regarding whether such a scaling is a passive operation).