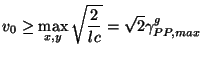Extension to (2+1)D

We briefly note that the same approach can be easily extended to the parallel-plate problem as well; beginning from system (3.67), we can introduce new variables

$$\tilde{i}_{1} = \sqrt{Z}i_{x}\hspace{0.5in}\tilde{i}_{2} = \sqrt{Z}i_{y}\hspace{0.5in}\tilde{i}_{3} = u/\sqrt{Z}$$

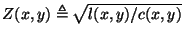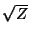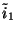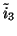where $Z(x,y) \triangleq \sqrt{l(x,y)/c(x,y)}$, and then multiply (3.67a) and (3.67b) by $1/\sqrt{Z}$ and (3.67c) by $\sqrt{Z}$. The new system is again symmetric hyperbolic. We do not show the network here, but we mention that we will require two gyrators; one linking the series adaptors with associated currents $\tilde{i}_{1}$ and $\tilde{i}_{3}$, the other between the adaptors for 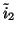$\tilde{i}_{2}$ and $\tilde{i}_{3}$. 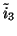One reflection-free port must be chosen for each gyrator; choosing both reflection-free ports at the adaptor with current 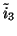$\tilde{i}_{3}$ must be ruled out, but other configurations are acceptable.

The stability bound for the balanced (2+1)D network will be

$$v_{0}\geq \max_{x,y}\sqrt{\frac{2}{lc}} = \sqrt{2}\gamma_{PP,max}^{g}$$

which is superior to (3.71), the bound for the standard form.