


Next: Finite Difference Interpretation
Up: The (2+1)D Parallel-plate System
Previous: Phase and Group Velocity
MDKC and MDWD Network
The circuit can be derived along the same lines as for the (1+1)D case; we deal here with the discretization on a rectilinear grid, and will thus apply coordinate transformation defined by the 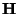 of (3.22). Rewriting system (3.67) in terms of the new coordinates
of (3.22). Rewriting system (3.67) in terms of the new coordinates
![$ [t_{1},\hdots, t_{5}]^{T}$](img867.png) using
using
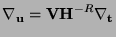 , with the pseudo inverse (3.23) gives
, with the pseudo inverse (3.23) gives
where we have used the new current-like variables
and 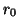 is, as in the (1+1)D case, an arbitrary positive constant (which has also been used to scale (3.69c)).
is, as in the (1+1)D case, an arbitrary positive constant (which has also been used to scale (3.69c)).
 will be treated as a simple time derivative, according to the generalized trapezoid rule discussed in §3.5.1. Figure 3.17 shows the MDKC that results from the transformed set of equations (3.69). The MDWD network corresponding to the MDKC is shown in Figure 3.18, where we have used step-sizes
will be treated as a simple time derivative, according to the generalized trapezoid rule discussed in §3.5.1. Figure 3.17 shows the MDKC that results from the transformed set of equations (3.69). The MDWD network corresponding to the MDKC is shown in Figure 3.18, where we have used step-sizes
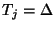 ,
,
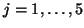 .
.
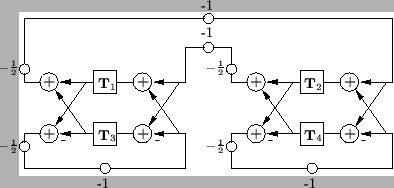
Figure 3.18:
MDWD network for the (2+1)D parallel-plate system, in rectangular coordinates.
|
Passivity follows from a positivity condition on the network inductances, in particular 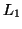 ,
, 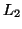 and
and 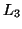 (the values of which are given in Figure 3.17). These conditions are
(the values of which are given in Figure 3.17). These conditions are
 |
(3.66) |
The choice of
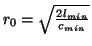 , where
, where
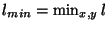 and
and
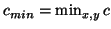 gives a stability bound of
gives a stability bound of
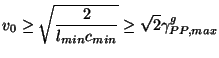 |
(3.67) |
which is the best possible bound for this network [61]. Note that 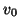 is again bounded away from the maximum group velocity, even taking into account the scaling factor (
is again bounded away from the maximum group velocity, even taking into account the scaling factor (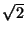 in this case), which is a consistent feature of explicit numerical methods in multiple spatial dimensions.
in this case), which is a consistent feature of explicit numerical methods in multiple spatial dimensions.
If  and
and  are constant, and in addition
are constant, and in addition 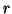 ,
, 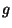 ,
, 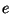 ,
, 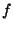 and
and 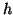 are zero, and (3.71) holds with equality, i.e., we have
are zero, and (3.71) holds with equality, i.e., we have
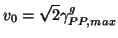 |
(3.68) |
then the network of Figure 3.18 simplifies to the structure shown in Figure 3.19. This particular structure bears a very strong resemblance to the (2+1)D waveguide mesh [157,198] which we saw briefly in §1.1.2, and will examine in detail in Chapter 4.
Figure 3.19:
Simplified MDWD network for the (2+1)D transmission line equations, in the lossless, source-free and constant parameter case.
 |



Next: Finite Difference Interpretation
Up: The (2+1)D Parallel-plate System
Previous: Phase and Group Velocity
Stefan Bilbao
2002-01-22
![]() and
and ![]() are constant, and in addition
are constant, and in addition ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are zero, and (3.71) holds with equality, i.e., we have
are zero, and (3.71) holds with equality, i.e., we have
