Next: MDKC and MDWD Network
Up: The (2+1)D Parallel-plate System
Previous: The (2+1)D Parallel-plate System
For the constant-coefficient, lossless and source-free case (i.e.,
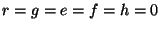 ), the numerical dispersion relation, in terms of the frequency
), the numerical dispersion relation, in terms of the frequency 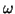 and wavenumber magnitude
and wavenumber magnitude

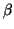
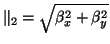 will be, from (3.10),
will be, from (3.10),
which has roots
Discounting the stationary mode with 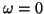 , the phase and group velocities are then, from (3.12),
, the phase and group velocities are then, from (3.12),
and if 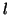 and
and 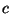 are functions of
are functions of 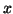 and
and 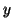 , the maximal group velocity will be
, the maximal group velocity will be
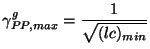 |
(3.64) |
where
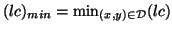 . This bound is the same as for the (1+1)D transmission line equations.
. This bound is the same as for the (1+1)D transmission line equations.
Figure 3.17:
MDKC for the (2+1)D parallel-plate system in rectangular coordinates.
|
|



Next: MDKC and MDWD Network
Up: The (2+1)D Parallel-plate System
Previous: The (2+1)D Parallel-plate System
Stefan Bilbao
2002-01-22
![]() ), the numerical dispersion relation, in terms of the frequency
), the numerical dispersion relation, in terms of the frequency ![]() and wavenumber magnitude
and wavenumber magnitude
![]()
![]()
![]() will be, from (3.10),
will be, from (3.10),