


Next: Phase and Group Velocity
Up: Multidimensional Wave Digital Filters
Previous: An Upwind Form
The (1+1)D Transmission Line
As a slightly more involved example, which highlights some of the issues which typically arise in the construction of these algorithms, consider the (1+1)D transmission line or telegrapher's equations [63]:
 |
(3.52a) |
Here, 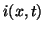 and
and 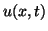 are the current and voltage in the transmission line,
are the current and voltage in the transmission line,  ,
,  ,
, 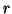 and
and 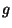 are inductance, capacitance, resistance and shunt conductance per unit length respectively, and are all non-negative functions of
are inductance, capacitance, resistance and shunt conductance per unit length respectively, and are all non-negative functions of  (
( and
and  are strictly positive
are strictly positive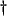 ).
). 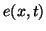 and
and 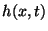 represent distributed voltage and current source terms. System (3.56) is symmetric hyperbolic; it has the form of (3.1), with
represent distributed voltage and current source terms. System (3.56) is symmetric hyperbolic; it has the form of (3.1), with
![$ {\bf w} = [i,u]^{T}$](img773.png) , and
, and
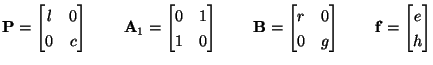 |
(3.53) |
Subsections
Stefan Bilbao
2002-01-22