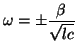Next: MDKC for the (1+1)D
Up: The (1+1)D Transmission Line
Previous: The (1+1)D Transmission Line
In the constant-coefficient case, where 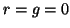 , the dispersion relation, defined in (3.10), will be
, the dispersion relation, defined in (3.10), will be
in terms of real frequencies 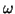 and wavenumbers
and wavenumbers  , and has solutions
, and has solutions
The phase and group velocities, from (3.12) are then
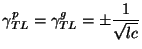 |
(3.54) |
and if  and
and  are functions of
are functions of  , the maximal group velocity will be
, the maximal group velocity will be
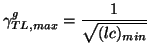 |
(3.55) |
where
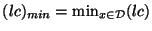 .
.
Stefan Bilbao
2002-01-22
![]() , the dispersion relation, defined in (3.10), will be
, the dispersion relation, defined in (3.10), will be