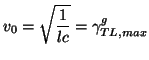Next: Energetic Interpretation
Up: The (1+1)D Transmission Line
Previous: Digression: Derivation of an
Returning to Figure 3.14(a), and making use of the discrete two-port derived in the last section, we can now write the complete wave digital network. It is shown in Figure 3.14(b).
Figure 3.14: (a) MD-passive network for the (1+1)D transmission line equations and (b) its associated MDWD network.
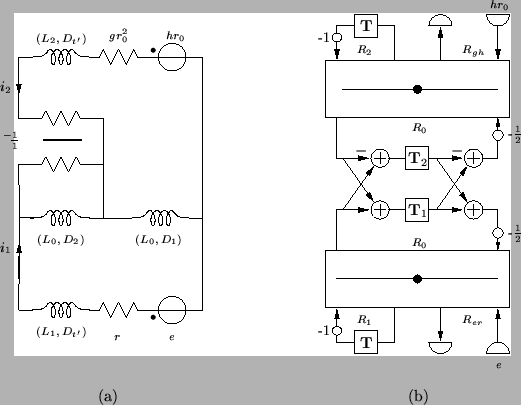 |
The inductances in the MDKC of Figure 3.14(a) are
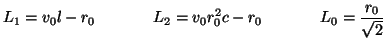 |
(3.59) |
and the port resistances of the MDWD network of Figure 3.14(b) are
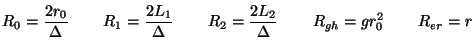 |
(3.60) |
The MDWD network is MD-passive if all the port resistances are non-negative over the entire spatial domain; from (3.63) and (3.64), the only port resistances which are possibly negative are 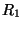 and
and 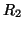 . Requiring their positivity gives the constraints
. Requiring their positivity gives the constraints
where
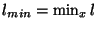 and
and
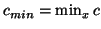 .
A judicious choice of
.
A judicious choice of
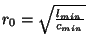 [131] allows the largest possible time step for a given grid spacing; the condition is then
[131] allows the largest possible time step for a given grid spacing; the condition is then
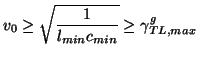 |
(3.61) |
where
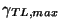 is defined by (3.59).
is defined by (3.59).
If  and
and  are constant, and (3.65) holds with equality, so that we have
are constant, and (3.65) holds with equality, so that we have
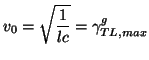 |
(3.62) |
then the MDWD numerical scheme is said to be operating at the Courant-Friedrichs-Lewy (CFL) bound [176]. For varying coefficients, however, 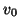 is bounded away from
is bounded away from
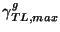 , so the time step will have to be chosen smaller than might be expected; we will look at how to improve upon this bound in §3.12.
, so the time step will have to be chosen smaller than might be expected; we will look at how to improve upon this bound in §3.12.



Next: Energetic Interpretation
Up: The (1+1)D Transmission Line
Previous: Digression: Derivation of an
Stefan Bilbao
2002-01-22


![]() and
and ![]() . Requiring their positivity gives the constraints
. Requiring their positivity gives the constraints
![]() and
and ![]() are constant, and (3.65) holds with equality, so that we have
are constant, and (3.65) holds with equality, so that we have