


Next: Boundary Conditions
Up: Multidimensional Wave Digital Filters
Previous: Numerical Phase Velocity and
Initial Conditions
Numerical simulations for time-dependent systems of PDEs must necessarily be initialized; while this is a relatively straightforward matter for WDF-based integration schemes, it has only been addressed in passing [106] in the literature.
We will examine here the initialization of the MDWD network for the source-free transmission line system (3.56) with 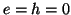 . This system requires initial distributions for both the current and voltage, which we will call
. This system requires initial distributions for both the current and voltage, which we will call 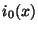 and
and 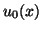 , respectively. For the initialization of the MDWD network for this system (shown in Figure 3.22), we will also need their spatial derivatives (assuming they exist), which we will write as
, respectively. For the initialization of the MDWD network for this system (shown in Figure 3.22), we will also need their spatial derivatives (assuming they exist), which we will write as 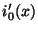 and
and 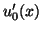 . We note that in the approach considered in [106], spatial derivative information has not been taken into account.
. We note that in the approach considered in [106], spatial derivative information has not been taken into account.
Figure 3.22:
MDWD network for the source-free (1+1)D transmission line equations.
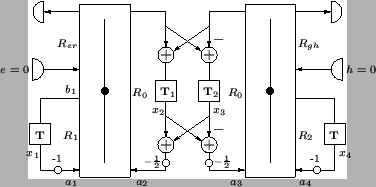 |
For the MDWD network of Figure 3.22, we must initialize all the wave variables incident upon the scattering junctions, written as 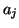 ,
,
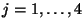 ; because we have assumed no sources, no wave enters through the loss/source port. This circuit is a MD representation, and each of these wave variables refers to an array. Assuming that the spatial grid spacing is
; because we have assumed no sources, no wave enters through the loss/source port. This circuit is a MD representation, and each of these wave variables refers to an array. Assuming that the spatial grid spacing is  , and the time step is
, and the time step is 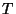 , we can index the elements of these arrays as
, we can index the elements of these arrays as 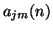 , for
, for 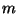 and
and  integer; this represents an instance of the MD wave variable
integer; this represents an instance of the MD wave variable 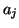 at grid location
at grid location 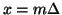 , and at time
, and at time 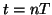 . For initialization, we must thus set
. For initialization, we must thus set 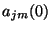 , over all grid locations
, over all grid locations 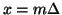 included in the domain of the problem, in terms of the quantities
included in the domain of the problem, in terms of the quantities
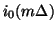 ,
,
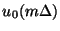 and their spatial derivatives.
and their spatial derivatives.
We will consider only the settings for the wave variables in the left-hand adaptor; one proceeds in the same way for the right adaptor. We recall that the port resistances are defined by
Since the port resistances 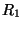 and
and 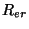 are functions of position, we will write
are functions of position, we will write
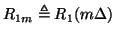 and
and
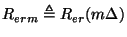 .
. 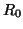 is independent of
is independent of  .
It is easy to see, from (2.30), that the initial values
.
It is easy to see, from (2.30), that the initial values 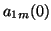 and
and 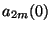 must be arranged such that we produce the initial current
must be arranged such that we produce the initial current
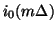 . Thus we need
. Thus we need
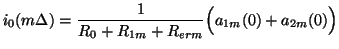 |
(3.87) |
Another condition is required to fully specify the wave variable initial values. Referring to the generating MDKC for this MDWD network in Figure 3.14(a), we can see that the voltage across the inductor of inductance 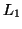 will be
will be
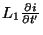 . We intend to relate this voltage to the associated digital voltage across the inductor of port resistance
. We intend to relate this voltage to the associated digital voltage across the inductor of port resistance 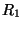 in Figure 3.22.
We have
in Figure 3.22.
We have
At time 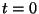 , and at location
, and at location 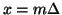 , we may write this voltage as
, we may write this voltage as
The wave digital voltage across the same port, at location 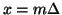 is defined by
is defined by
 |
(3.91) |
Thus, for initialization, equating the voltages in (3.88) and (3.87), we must have
This requirement, along with (3.86) fully specifies the initial values of the wave variables at the left adaptor. We thus have
We note that
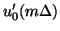 may be obtained from the initial voltage distribution
may be obtained from the initial voltage distribution 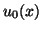 by any reasonable (i.e., consistent) approximation to the spatial derivative.
by any reasonable (i.e., consistent) approximation to the spatial derivative.
It is important to recognize that for constant 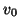 , we have
, we have
These values occur in the same ratio as those of an eigenvector of the scattering matrix for the left series adaptor. In particular, they follow the distribution of the principal eigenvector (i.e., the unique eigenvector whose elements are all of the same sign) of the scattering matrix. Thus the proper setting for the initial conditions (except at the loss port) should be aligned with the dominant mode of the numerical scheme in this limit (and the fraction of the initial energy injected into the parasitic modes will vanish)--see §3.9.2 for a discussion of parasitic modes in this particular system . We also suggest the following very simple ``rule of thumb'' for setting initial conditions:
. We also suggest the following very simple ``rule of thumb'' for setting initial conditions:
This rule is to be interpreted in a distributed sense, i.e., it holds for every instance of an adaptor on the numerical grid. A similar rule holds for a parallel adaptor. These settings ignore spatial derivative information, but give a simple way of proceeding in general, especially during the first stages of programming and debugging, and are correct (to first order) in the limit as  approaches 0. If losses are large, though, one may prefer to use exact conditions like (3.89). This rule applies regardless of the number of dimensions of the problem (but may need to be amended if sources or reflection-free ports are present).
approaches 0. If losses are large, though, one may prefer to use exact conditions like (3.89). This rule applies regardless of the number of dimensions of the problem (but may need to be amended if sources or reflection-free ports are present).



Next: Boundary Conditions
Up: Multidimensional Wave Digital Filters
Previous: Numerical Phase Velocity and
Stefan Bilbao
2002-01-22
![]() . This system requires initial distributions for both the current and voltage, which we will call
. This system requires initial distributions for both the current and voltage, which we will call ![]() and
and ![]() , respectively. For the initialization of the MDWD network for this system (shown in Figure 3.22), we will also need their spatial derivatives (assuming they exist), which we will write as
, respectively. For the initialization of the MDWD network for this system (shown in Figure 3.22), we will also need their spatial derivatives (assuming they exist), which we will write as ![]() and
and ![]() . We note that in the approach considered in [106], spatial derivative information has not been taken into account.
. We note that in the approach considered in [106], spatial derivative information has not been taken into account.
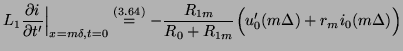
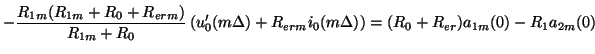
![]() , we have
, we have

![]() approaches 0. If losses are large, though, one may prefer to use exact conditions like (3.89). This rule applies regardless of the number of dimensions of the problem (but may need to be amended if sources or reflection-free ports are present).
approaches 0. If losses are large, though, one may prefer to use exact conditions like (3.89). This rule applies regardless of the number of dimensions of the problem (but may need to be amended if sources or reflection-free ports are present).