Finite Difference Schemes for the Wave Equation

In this appendix, we reexamine the finite difference schemes corresponding to the waveguide meshes discussed in Chapter 4, in the special case for which the underlying model problem is lossless, source-free and does not exhibit any material parameter variation. In this case, these finite difference schemes will solve the wave equation, given by

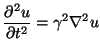$$\frac{\partial^{2} u}{\partial t^{2}} = \gamma^{2}\nabla^{2}u$$ (A.1)

in either (2+1)D or (3+1)D, depending on the type of mesh. Here, 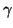$\gamma$ is the wave speed, and 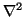$\nabla^{2}$ is the Laplacian [174]. These schemes will be linear and shift-invariant, and as such, it is possible to analyze them in the frequency domain, through what is called Von Neumann analysis [176]. We will apply these methods to the rectilinear, interpolated rectilinear, triangular, hexagonal and fourth-order accurate schemes in (2+1)D, then to the cubic rectilinear, interpolated cubic rectilinear, octahedral and tetrahedral schemes in (3+1)D.