


Next: Finite Difference Schemes for
Up: Von Neumann Analysis of
Previous: Vector Schemes
Numerical Phase Velocity
For a given amplification factor
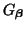 , the numerical phase velocity at frequency
, the numerical phase velocity at frequency
 is defined by
is defined by
where


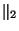 is the Euclidean norm of the vector
is the Euclidean norm of the vector
 . This expression gives the speed of propagation for a plane wave of wavenumber
. This expression gives the speed of propagation for a plane wave of wavenumber  , according to the numerical scheme for which
, according to the numerical scheme for which
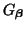 is an amplification factor. For the wave equation model problem, the speed of any plane wave solution will simply be
is an amplification factor. For the wave equation model problem, the speed of any plane wave solution will simply be 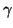 , but the numerical phase velocity will in general be different, and in particular, wave speeds will be directionally-dependent to a certain degree, depending on the type of scheme used. For all these schemes, the numerical phase velocity for at least one of the amplification factors will approach the correct physical velocity near the spatial DC frequency, by consistency of the numerical scheme with the wave equation
, but the numerical phase velocity will in general be different, and in particular, wave speeds will be directionally-dependent to a certain degree, depending on the type of scheme used. For all these schemes, the numerical phase velocity for at least one of the amplification factors will approach the correct physical velocity near the spatial DC frequency, by consistency of the numerical scheme with the wave equation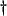 .
.
Stefan Bilbao
2002-01-22

