


Next: Numerical Phase Velocity
Up: Von Neumann Analysis of
Previous: Multi-step Schemes
For two of the schemes that we will examine (hexagonal and tetrahedral), it will be necessary to analyze a vectorized system of difference equations. In general, the analysis of vector forms is considerably more difficult; the typical approach will invoke the Kreiss Matrix Theorem [176], which is a set of equivalent conditions which can be used to check the boundedness of a particular amplification matrix. In the general vector case we will be analyzing the evolution of a 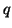 -element vector
-element vector
![$ \hat{{\bf U}}_{\mbox{{\scriptsize\boldmath $\beta$}}}(n) = [\hat{U}_{1,\mbox{{...
...\beta$}}}(n), \hdots, \hat{U}_{q,\mbox{{\scriptsize\boldmath $\beta$}}}(n)]^{T}$](img2839.png) of spatially Fourier-transformed functions of
of spatially Fourier-transformed functions of
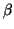 . The
. The 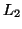 norm is defined by
norm is defined by
where 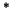 denotes transpose conjugation.
denotes transpose conjugation.
The schemes for the wave equation that we will examine, however, have a relatively simple form. The column vector of grid spatial frequency spectra
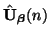 satisfies an equation of the form
satisfies an equation of the form
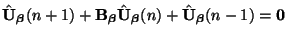 |
(A.11) |
for some Hermitian matrix function of
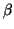 ,
,
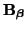 . Because
. Because
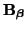 is Hermitian, we may write
is Hermitian, we may write
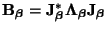 , for some unitary matrix
, for some unitary matrix
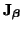 , and a real diagonal matrix
, and a real diagonal matrix
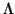
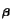 containing the eigenvalues of
containing the eigenvalues of
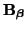 . As such, we may change variables via
. As such, we may change variables via
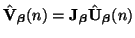 , to get
, to get
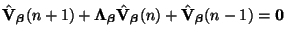 |
(A.12) |
The system thus decouples into a system of scalar two-step spectral update equations; because
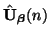 and
and
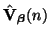 are related by a unitary transformation, we have
are related by a unitary transformation, we have
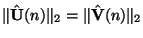 , and we may apply stability tests to the uncoupled system (A.11). We thus require that the eigenvalues of
, and we may apply stability tests to the uncoupled system (A.11). We thus require that the eigenvalues of
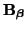 , namely
, namely
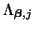 for
for
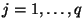 , which are the elements on the diagonal of
, which are the elements on the diagonal of
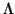
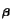 , all satisfy
, all satisfy
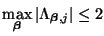 |
(A.13) |
At frequencies
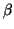
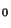 for which any of the eigenvalues satisfies (A.12) with equality, then we may again have the same problem with mild linear growth in the solution.
for which any of the eigenvalues satisfies (A.12) with equality, then we may again have the same problem with mild linear growth in the solution.



Next: Numerical Phase Velocity
Up: Von Neumann Analysis of
Previous: Multi-step Schemes
Stefan Bilbao
2002-01-22
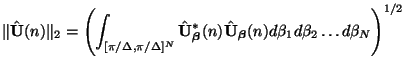
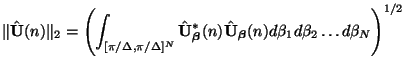
![]() satisfies an equation of the form
satisfies an equation of the form