


Next: One-step Schemes
Up: Finite Difference Schemes for
Previous: Finite Difference Schemes for
Von Neumann Analysis of Difference Schemes
In this section, we summarize the basics of Von Neumann analysis provided in [176]. Consider the ( +1)D real-valued grid function
+1)D real-valued grid function
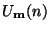 , defined for integer
, defined for integer  and for
and for
![$ {\bf m} = [m_{1},\hdots,m_{N}] \in \mathbb{Z}^{N}$](img2783.png) , the set of all integer
, the set of all integer  -tuples. Such a grid function will be used, in a finite difference scheme, as an approximation to the continuous solution
-tuples. Such a grid function will be used, in a finite difference scheme, as an approximation to the continuous solution
 to some problem, at the location
to some problem, at the location
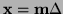 , and at time
, and at time 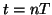 , where
, where  is the grid spacing, and
is the grid spacing, and 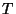 is the time step. Here, and henceforth in this appendix, we have assumed that the grid spacing is uniform in all the spatial coordinates, and that the spatial domain is unbounded. As in Chapters 3 and 4, we define the space step/time step ratio to be
is the time step. Here, and henceforth in this appendix, we have assumed that the grid spacing is uniform in all the spatial coordinates, and that the spatial domain is unbounded. As in Chapters 3 and 4, we define the space step/time step ratio to be
The spatial Fourier transform of
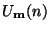 is defined by
is defined by
and is a periodic function of 
![$ =[\beta_{1},\hdots,\beta_{N}]^{T}$](img2787.png) , a vector of spatial wavenumbers. The transform can be inverted by
, a vector of spatial wavenumbers. The transform can be inverted by
where 
![$ \in[-\pi/\Delta, \pi/\Delta]^{N}$](img2789.png) refers to the space enclosed by the intervals
refers to the space enclosed by the intervals
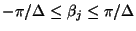 , for
, for
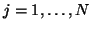 .
If, for a given grid spacing
.
If, for a given grid spacing  , we define the discrete spatial
, we define the discrete spatial 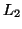 norm of
norm of
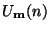 by
by
and the corresponding spectral 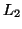 norm of
norm of
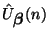 by
by
then if
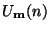 and
and
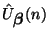 are in their respective
are in their respective 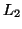 spaces, Parseval's relation gives
spaces, Parseval's relation gives
Subsections



Next: One-step Schemes
Up: Finite Difference Schemes for
Previous: Finite Difference Schemes for
Stefan Bilbao
2002-01-22
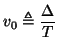
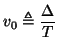
![]() is defined by
is defined by
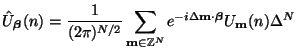
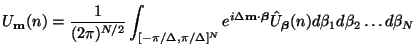

![$\displaystyle \Vert\hat{U}(n)\Vert _{2} = \left(\int_{[-\pi/\Delta, \pi/\Delta]...
...ldmath$\beta$}}}(n)\vert^{2}d\beta_{1} d\beta_{2}\hdots d\beta_{N}\right)^{1/2}$](img2793.png)