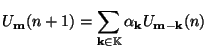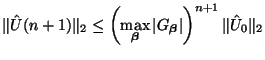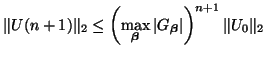One-step Schemes

Consider the following one-step explicit difference scheme, which relates values of the grid function 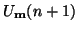$U_{{\bf m}}(n+1)$ to values at the previous time step:

$$U_{{\bf m}}(n+1) = \sum_{{\bf k}\in \mathbb{K}}\alpha_{{\bf k}}U_{{\bf m - k}}(n)$$

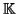where $\mathbb{K}$ is some subset of 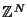$\mathbb{Z}^{N}$, and the parameters 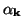$\alpha_{{\bf k}}$ are constants; it is initialized by setting 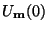$U_{{\bf m}}(0)$ equal to some function 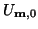$U_{{\bf m},0}$ (assumed to be in 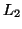$L_{2}$). Taking the spatial Fourier transform of this recursion gives

$$\hat{U}_{\mbox{{\scriptsize\boldmath$\beta$}}}(n+1) = \left(\sum_{{\bf k}\in \mathbb{K}}\alpha_{{\bf k}}e^{-j\Delta{\bf... ...oldmath$\beta$}}}\right)\hat{U}_{\mbox{{\scriptsize\boldmath$\beta$}}}(n)\notag$$ (A.2)

$$= \hspace{0.5in}G_{\mbox{{\scriptsize\boldmath$\beta$}}}\hspace{0.44in}\hat{U}_{\mbox{{\scriptsize\boldmath$\beta$}}}(n)$$ (A.3)

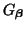$G_{\mbox{{\scriptsize\boldmath $\beta$}}}$ so defined is called the spectral amplification factor for a one-step finite difference scheme. (A.2) implies that we have, in particular, that

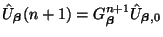$$\hat{U}_{\mbox{{\scriptsize\boldmath$\beta$}}}(n+1) = G_{\mbox{{\... ...ptsize\boldmath$\beta$}}}^{n+1}\hat{U}_{\mbox{{\scriptsize\boldmath$\beta$}},0}$$ (A.4)

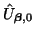where $\hat{U}_{\mbox{{\scriptsize\boldmath $\beta$}},0}$ is the spatial Fourier transform of the initial condition 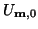$U_{{\bf m},0}$. (A.3) further implies that

$$\Vert\hat{U}(n+1)\Vert _{2} \leq \left(\max_{\mbox{{\scriptsize\b... ...box{{\scriptsize\boldmath$\beta$}}}\vert\right)^{n+1}\Vert\hat{U}_{0}\Vert _{2}$$

and finally, through Parseval's relation, that

$$\Vert U(n+1)\Vert _{2} \leq \left(\max_{\mbox{{\scriptsize\boldma... ...G_{\mbox{{\scriptsize\boldmath$\beta$}}}\vert\right)^{n+1}\Vert U_{0}\Vert _{2}$$

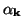If the $\alpha_{{\bf k}}$ which define the difference scheme are independent of the grid spacing and the time step, then such a difference scheme is called stable if

$$\max_{\mbox{{\scriptsize\boldmath$\beta$}}}\vert G_{\mbox{{\scriptsize\boldmath$\beta$}}}\vert\leq 1$$

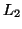The $L_{2}$ norm of the solution to the difference equation will thus not increase as the simulation progresses.