


Next: The Tetrahedral Scheme
Up: Finite Difference Schemes for
Previous: The Octahedral Scheme
The (3+1)D Interpolated Rectilinear Scheme
In the interest of achieving a more uniform numerical dispersion profile in (3+1)D, it is of course possible to define an interpolated scheme [155,158], in the same way as was done in (2+1)D in §A.2.2. We will again have a two-step scheme, and updating at a given grid point is performed with reference to, at the previous time step, the grid point at the same location, as well as the 26 nearest neighbors: the six points a distance  away, twelve points at a distance of
away, twelve points at a distance of
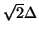 , and eight points that are
, and eight points that are
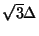 away--see Figure A.11(a). We present here a complete analysis of the relevant stability conditions, as well as the conditions under which a waveguide mesh implementation exists. We also look at a means of minimizing directional dependence of the numerical dispersion.
away--see Figure A.11(a). We present here a complete analysis of the relevant stability conditions, as well as the conditions under which a waveguide mesh implementation exists. We also look at a means of minimizing directional dependence of the numerical dispersion.
Like the cubic rectilinear and octahedral schemes, this scheme will be defined over a rectilinear grid indexed by  ,
,  and
and  and will have the general form
and will have the general form
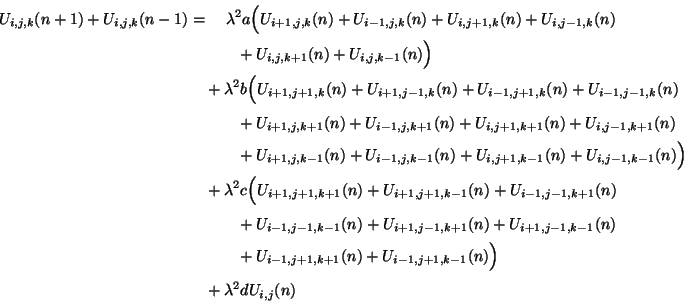 |
(A.31) |
In order for scheme (A.30) to satisfy the wave equation, we require the constants  ,
, 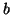 ,
,  and
and 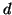 to satisfy the constraints
to satisfy the constraints
 |
(A.32) |
and a family of difference schemes parametrized by  ,
, 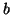 and
and 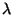 results.
results.
The stability analysis of this scheme proceeds along the same lines as that of the (2+1)D scheme, though as we shall see, the stability condition on the parameters  and
and 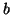 is considerably more complex. As before, we have an amplification polynomial of the form of (A.5), now with
is considerably more complex. As before, we have an amplification polynomial of the form of (A.5), now with
where as before,
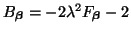 . Because
. Because
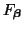 is again multilinear in the three cosines, its extrema can only occur at the eight corners of the cubic region defined by
is again multilinear in the three cosines, its extrema can only occur at the eight corners of the cubic region defined by
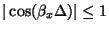 ,
,
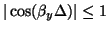 and
and
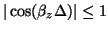 . These extrema are
. These extrema are
The non-positivity requirement on
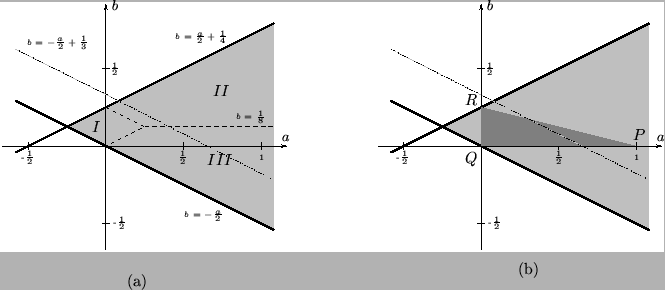
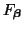 then amounts to requiring that these extreme values be non-positive. The resulting stability region in the
then amounts to requiring that these extreme values be non-positive. The resulting stability region in the 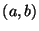 plane is shown in grey in Figure A.10(a).
plane is shown in grey in Figure A.10(a).
Figure A.10: (a) Stability region, in grey, for the interpolated rectilinear scheme, plotted in the 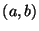 plane. This region can be divided into three sub-regions, labeled
plane. This region can be divided into three sub-regions, labeled  ,
, 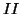 , and
, and 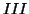 separated by dashed lines, over which different stability conditions on
separated by dashed lines, over which different stability conditions on 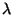 apply. In region
apply. In region  , we must have
, we must have
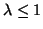 , in region
, in region 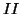
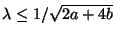 , and in region
, and in region 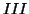
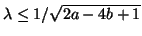 . The dotted line indicates choices of
. The dotted line indicates choices of  and
and 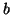 for which numerical dispersion is optimally direction-independent. (b) The subset of stable schemes for which a passive waveguide mesh implementation exists is shown in dark grey. Over this region, we require
for which numerical dispersion is optimally direction-independent. (b) The subset of stable schemes for which a passive waveguide mesh implementation exists is shown in dark grey. Over this region, we require
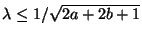 . This bound is more strict than the stability conditions mentioned above in the same region. We also remark that this interpolated scheme reduces to other simpler schemes under particular choices of
. This bound is more strict than the stability conditions mentioned above in the same region. We also remark that this interpolated scheme reduces to other simpler schemes under particular choices of  and
and 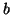 . At point
. At point 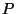 , we have the cubic rectilinear scheme (see §A.3.1), at point
, we have the cubic rectilinear scheme (see §A.3.1), at point 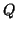 we have the octahedral scheme (see §A.3.2), and at point
we have the octahedral scheme (see §A.3.2), and at point 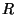 we have what might be called a ``dodecahedral'' scheme. Notice in particular that none of these schemes is optimally direction-independent (i.e.,
we have what might be called a ``dodecahedral'' scheme. Notice in particular that none of these schemes is optimally direction-independent (i.e., 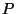 ,
, 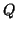 and
and 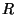 do not lie on the dotted line).
do not lie on the dotted line).
 |
Assuming that  and
and 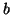 fall in this region, we must now find the values of
fall in this region, we must now find the values of 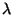 which satisfy (A.9). The minimum value of
which satisfy (A.9). The minimum value of
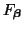 depends on
depends on  and
and 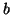 in a non-trivial way; referring to Figure A.10(a), the stability domain can be divided into three regions, and in each there is a different closed form expression for the upper bound on
in a non-trivial way; referring to Figure A.10(a), the stability domain can be divided into three regions, and in each there is a different closed form expression for the upper bound on 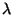 . These bounds are given explicitly in the caption to Figure A.10(a).
. These bounds are given explicitly in the caption to Figure A.10(a).
In order to examine the directional dependence of the dispersion error, we may expand
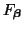 in a Taylor series about
in a Taylor series about 
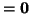 , as was done in the (2+1)D case. We have
, as was done in the (2+1)D case. We have
which implies that
and the dispersion error is directionally-independent to fourth order. This special choice of the parameters  and
and 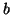 is plotted as a dotted line in Figure A.10(a). It is well worth comparing this optimization method with the computer-based techniques applied to the same problem in [158].
is plotted as a dotted line in Figure A.10(a). It is well worth comparing this optimization method with the computer-based techniques applied to the same problem in [158].
The computational and add densities for the scheme will be
Considerable computational savings are possible if any of  ,
, 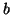 ,
,  or
or 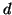 is zero.
is zero.
Finally, we remark that the (3+1)D interpolated scheme can be realized as a waveguide mesh, where, at any given junction, we will have four types of waveguide connections: those of admittances 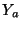 ,
, 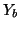 and
and 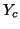 are connected to the neighboring junctions located at gridpoints at distances
are connected to the neighboring junctions located at gridpoints at distances  ,
,
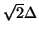 and
and
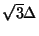 away respectively, and a self-loop of admittance
away respectively, and a self-loop of admittance 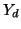 is also connected to every junction. We end up with exactly difference scheme (A.30), with
is also connected to every junction. We end up with exactly difference scheme (A.30), with
The passivity condition is then a positivity condition on these admittances, and thus on the parameters  ,
, 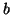 ,
,  and
and 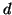 . Recalling the expression for
. Recalling the expression for  in terms of
in terms of  and
and 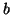 from (A.31), we must have
from (A.31), we must have
This region is shown, in dark grey, in Figure A.10(b). The positivity condition on 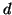 (expressed in terms of
(expressed in terms of  ,
, 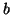 and
and 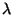 as per (A.31)) gives the bound on
as per (A.31)) gives the bound on 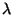 , which is
, which is
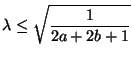 (for passivity) (for passivity) |
|
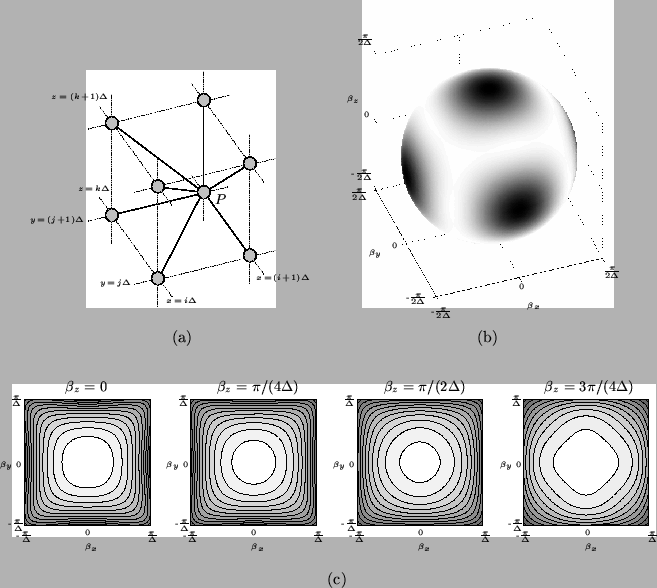
Figure A.11:
The (3+1)D interpolated rectilinear scheme (A.30)-- (a) numerical grid and connections, from a central grid point (labeled P) to its neighbors in one octant. (b)
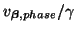 for the scheme with
for the scheme with 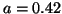 and
and 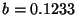 at the stability bound
at the stability bound
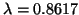 , for a spherical surface with
, for a spherical surface with


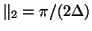 --the shading is normalized over the surface so that white and black refer to minimal and maximal dispersion error, respectively. Here, unlike for the cubic rectilinear and octahedral schemes, there are no dispersionless directions. The variation in the numerical phase velocity is, however, quite small, ranging from 96.81 to 97.32 per cent of the correct wave speed. (c) Contour plots of
--the shading is normalized over the surface so that white and black refer to minimal and maximal dispersion error, respectively. Here, unlike for the cubic rectilinear and octahedral schemes, there are no dispersionless directions. The variation in the numerical phase velocity is, however, quite small, ranging from 96.81 to 97.32 per cent of the correct wave speed. (c) Contour plots of
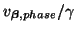 for various cross-sections of the space of spatial frequencies
for various cross-sections of the space of spatial frequencies
 ; contours indicate successive deviations of 2 per cent from the ideal value of 1 which is obtained at spatial DC.
; contours indicate successive deviations of 2 per cent from the ideal value of 1 which is obtained at spatial DC.
 |



Next: The Tetrahedral Scheme
Up: Finite Difference Schemes for
Previous: The Octahedral Scheme
Stefan Bilbao
2002-01-22
![]() away, twelve points at a distance of
away, twelve points at a distance of
![]() , and eight points that are
, and eight points that are
![]() away--see Figure A.11(a). We present here a complete analysis of the relevant stability conditions, as well as the conditions under which a waveguide mesh implementation exists. We also look at a means of minimizing directional dependence of the numerical dispersion.
away--see Figure A.11(a). We present here a complete analysis of the relevant stability conditions, as well as the conditions under which a waveguide mesh implementation exists. We also look at a means of minimizing directional dependence of the numerical dispersion.
![]() ,
, ![]() and
and ![]() and will have the general form
and will have the general form
![]() and
and ![]() is considerably more complex. As before, we have an amplification polynomial of the form of (A.5), now with
is considerably more complex. As before, we have an amplification polynomial of the form of (A.5), now with
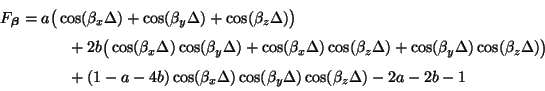

![]() and
and ![]() fall in this region, we must now find the values of
fall in this region, we must now find the values of ![]() which satisfy (A.9). The minimum value of
which satisfy (A.9). The minimum value of
![]() depends on
depends on ![]() and
and ![]() in a non-trivial way; referring to Figure A.10(a), the stability domain can be divided into three regions, and in each there is a different closed form expression for the upper bound on
in a non-trivial way; referring to Figure A.10(a), the stability domain can be divided into three regions, and in each there is a different closed form expression for the upper bound on ![]() . These bounds are given explicitly in the caption to Figure A.10(a).
. These bounds are given explicitly in the caption to Figure A.10(a).
![]() in a Taylor series about
in a Taylor series about ![]()
![]() , as was done in the (2+1)D case. We have
, as was done in the (2+1)D case. We have
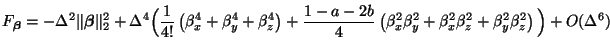
![]() ,
, ![]() and
and ![]() are connected to the neighboring junctions located at gridpoints at distances
are connected to the neighboring junctions located at gridpoints at distances ![]() ,
,
![]() and
and
![]() away respectively, and a self-loop of admittance
away respectively, and a self-loop of admittance ![]() is also connected to every junction. We end up with exactly difference scheme (A.30), with
is also connected to every junction. We end up with exactly difference scheme (A.30), with
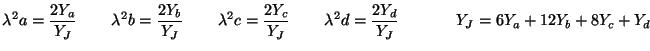
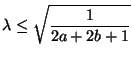 (for passivity)
(for passivity)