


Next: The Octahedral Scheme
Up: Finite Difference Schemes for
Previous: Finite Difference Schemes for
The Cubic Rectilinear Scheme
This is the simplest scheme for the (3+1)D wave equation. The grid points, indexed by  ,
, 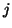 and
and  are located at coordinates
are located at coordinates
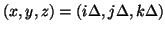 . The finite difference scheme is written as
. The finite difference scheme is written as
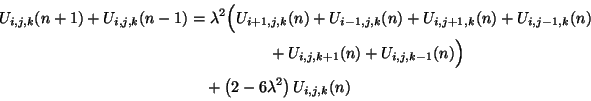 |
(A.29) |
If the grid points are located at the corners of a cubic lattice, then updating the scheme requires access to the grid function at the six neighboring corners; see Figure A.8(a).
The stability analysis is very similar to that of the (2+1)D rectilinear scheme, except that we now have a 3-tuple of spatial frequencies,

![$ = [\beta_{x}, \beta_{y}, \beta_{z}]^{T}$](img3045.png) . The amplification polynomial equation is again of the form of (A.5), with
. The amplification polynomial equation is again of the form of (A.5), with
and thus
Because
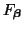 is multilinear in the cosines, it is simple to show that
is multilinear in the cosines, it is simple to show that
and so, from (A.9),
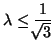 (for Von Neumann stability) (for Von Neumann stability) |
|
When
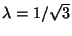 , the amplification factors become degenerate and linear growth of the solution may occur for
, the amplification factors become degenerate and linear growth of the solution may occur for
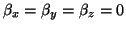 , and for
, and for
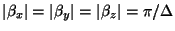 . The computational and add densities are
. The computational and add densities are
for
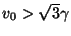 , and
, and
at the stability limit
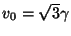 . At this limit, the scheme may, like the (2+1)D scheme, be divided into two mutually exclusive subschemes. See Figure A.8(b) and (c) for plots of the numerical dispersion properties of the cubic rectilinear scheme.
. At this limit, the scheme may, like the (2+1)D scheme, be divided into two mutually exclusive subschemes. See Figure A.8(b) and (c) for plots of the numerical dispersion properties of the cubic rectilinear scheme.
Figure A.8:
The cubic rectilinear scheme (A.28)-- (a) numerical grid and connections, where grey/white coloring of points indicates a division into mutually exclusive subschemes at the stability bound; (b)
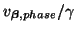 for the scheme at the stability bound
for the scheme at the stability bound
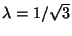 , for a spherical surface with
, for a spherical surface with


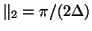 --the shading is normalized over the surface so that white corresponds to no dispersion error, and black to the maximum error over the surface (which is 7 per cent in this case). (c) Contour plots of
--the shading is normalized over the surface so that white corresponds to no dispersion error, and black to the maximum error over the surface (which is 7 per cent in this case). (c) Contour plots of
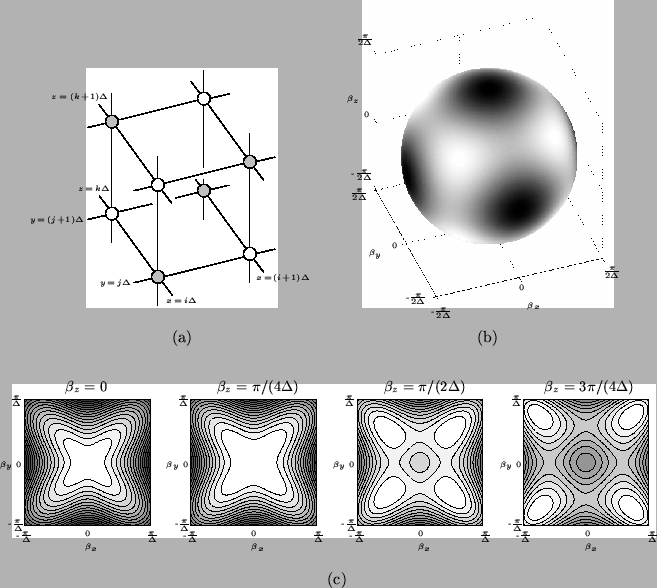
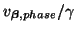 for various cross-sections of the space of spatial frequencies
for various cross-sections of the space of spatial frequencies
 ; contours indicate successive deviations of 2 per cent from the ideal value of 1 which is obtained at spatial DC.
; contours indicate successive deviations of 2 per cent from the ideal value of 1 which is obtained at spatial DC.
 |



Next: The Octahedral Scheme
Up: Finite Difference Schemes for
Previous: Finite Difference Schemes for
Stefan Bilbao
2002-01-22
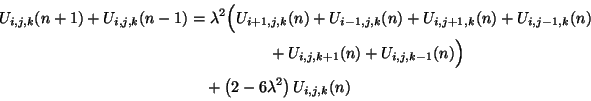
![]() , the amplification factors become degenerate and linear growth of the solution may occur for
, the amplification factors become degenerate and linear growth of the solution may occur for
![]() , and for
, and for
![]() . The computational and add densities are
. The computational and add densities are
