


Next: A (1+1)D Waveguide Network
Up: The (1+1)D Transmission Line
Previous: First-order System and the
Centered Difference Schemes and Grid Decimation
Suppose we are interested in developing a finite difference scheme to calculate the solution to (4.17) numerically. We first define grid functions 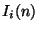 , and
, and 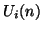 which, for convenience, will run over half-integer values of
which, for convenience, will run over half-integer values of  and
and  , i.e.,
, i.e.,
They are intended to approximate  and
and 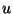 at the points
at the points
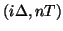 , where
, where  is the spatial grid step, and
is the spatial grid step, and 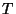 the time step. We note that we have used the same variable,
the time step. We note that we have used the same variable,  , to stand for both the continuous-time current which solves (4.17), as well as the discrete-valued variable representing the spatial coordinate on the grid.
, to stand for both the continuous-time current which solves (4.17), as well as the discrete-valued variable representing the spatial coordinate on the grid.
We have the centered difference approximations
 |
(4.19a) |
where 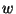 stands for either of
stands for either of  or
or 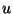 .
.
Employing these differences in (4.17), and replacing the continuous time/space variables  and
and 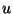 by their respective grid functions yields the difference scheme
by their respective grid functions yields the difference scheme
Here, we have chosen
for half-integer  . Because the centered difference approximations (4.19) are second-order accurate,
. Because the centered difference approximations (4.19) are second-order accurate,  and
and  may be approximated to the same order without any decrease in accuracy. We leave the exact form of these approximations,
may be approximated to the same order without any decrease in accuracy. We leave the exact form of these approximations, 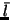 and
and 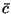 unspecified for the moment, but will return to various settings in §4.3.6. Also, in order to remain consistent with the notation in the MDWD schemes of the last chapter, we have set
unspecified for the moment, but will return to various settings in §4.3.6. Also, in order to remain consistent with the notation in the MDWD schemes of the last chapter, we have set
Thus difference equations (4.20) are consistent with (4.17), and accurate to
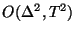 .
.
In a difference scheme for a general system of PDEs, it would be necessary to update all the grid functions every time step, and at every grid point--that is to say, at every increment in  and
and  of one-half, new values of the grid functions would have to be calculated, and indeed, we can proceed in this manner in with the scheme (4.20) as well. In this case, however, it is easy to see that updating
of one-half, new values of the grid functions would have to be calculated, and indeed, we can proceed in this manner in with the scheme (4.20) as well. In this case, however, it is easy to see that updating 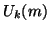 , for
, for 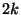 and
and 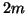 even requires access only to
even requires access only to 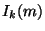 at the previous time step, and at neighboring grid locations (thus for
at the previous time step, and at neighboring grid locations (thus for 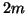 odd and
odd and 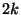 odd), as well as
odd), as well as 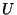 at the same location, two time steps previously (
at the same location, two time steps previously (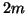 and
and 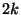 again even) [131,184]. Similarly, updating
again even) [131,184]. Similarly, updating 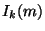 for
for 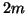 odd and
odd and 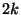 odd involves only values of
odd involves only values of 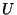 for
for 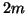 even and
even and 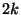 even, and
even, and  for
for 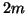 odd and
odd and 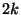 odd. It is then obvious that only values of
odd. It is then obvious that only values of 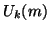 for which
for which 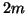 is even and
is even and 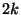 even (and values of
even (and values of 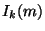 with
with 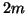 odd and
odd and 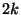 odd) need enter into our scheme. We can thus decimate the grid in the manner shown in Figure 4.7.
odd) need enter into our scheme. We can thus decimate the grid in the manner shown in Figure 4.7.
Figure 4.7:
Interleaved sampling grid for the (1+1)D transmission line.
 |
We calculate the values of 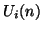 at the grey dots in Figure 4.7, and
at the grey dots in Figure 4.7, and
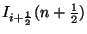 at the white dots. The difference scheme on the decimated grid can be written as
at the white dots. The difference scheme on the decimated grid can be written as
 |
(4.22a) |
for  ,
,  integer. We perform the calculation on the decimated grid with no decrease in accuracy, although we are of course approximating the solution at fewer grid points. In analogy with the continuous case, when
integer. We perform the calculation on the decimated grid with no decrease in accuracy, although we are of course approximating the solution at fewer grid points. In analogy with the continuous case, when  and
and  are constant it is possible to combine the difference equations (4.22) into a single equation for the voltage grid function
are constant it is possible to combine the difference equations (4.22) into a single equation for the voltage grid function 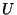 , which is
, which is
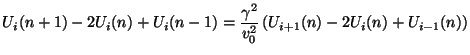 |
(4.23) |
and which solves the (1+1)D wave equation (4.18). For the so-called magic time step [184],
the difference scheme (4.23) reduces to
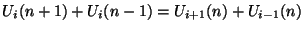 |
(4.24) |
a form which has great relevance to the discussion to follow on the waveguide implementation. It is interesting that in this case, the grid may be further decimated; we need only calculate 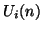 for
for 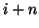 even (or odd), for
even (or odd), for  ,
,  integer. We will examine this point in further detail in higher dimensions in Appendix A.
integer. We will examine this point in further detail in higher dimensions in Appendix A.



Next: A (1+1)D Waveguide Network
Up: The (1+1)D Transmission Line
Previous: First-order System and the
Stefan Bilbao
2002-01-22
![]() and
and ![]() by their respective grid functions yields the difference scheme
by their respective grid functions yields the difference scheme
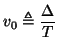
![]() and
and ![]() of one-half, new values of the grid functions would have to be calculated, and indeed, we can proceed in this manner in with the scheme (4.20) as well. In this case, however, it is easy to see that updating
of one-half, new values of the grid functions would have to be calculated, and indeed, we can proceed in this manner in with the scheme (4.20) as well. In this case, however, it is easy to see that updating ![]() , for
, for ![]() and
and ![]() even requires access only to
even requires access only to ![]() at the previous time step, and at neighboring grid locations (thus for
at the previous time step, and at neighboring grid locations (thus for ![]() odd and
odd and ![]() odd), as well as
odd), as well as ![]() at the same location, two time steps previously (
at the same location, two time steps previously (![]() and
and ![]() again even) [131,184]. Similarly, updating
again even) [131,184]. Similarly, updating ![]() for
for ![]() odd and
odd and ![]() odd involves only values of
odd involves only values of ![]() for
for ![]() even and
even and ![]() even, and
even, and ![]() for
for ![]() odd and
odd and ![]() odd. It is then obvious that only values of
odd. It is then obvious that only values of ![]() for which
for which ![]() is even and
is even and ![]() even (and values of
even (and values of ![]() with
with ![]() odd and
odd and ![]() odd) need enter into our scheme. We can thus decimate the grid in the manner shown in Figure 4.7.
odd) need enter into our scheme. We can thus decimate the grid in the manner shown in Figure 4.7.