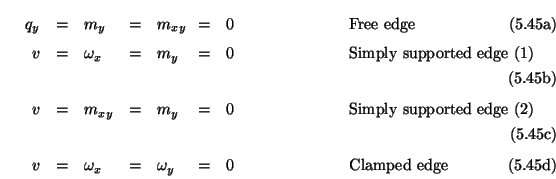 |
As we mentioned in §5.2.4, the passive boundary termination of an MDWD network, such as that shown in Figure 5.16, is not at all straightforward. Indeed, it is somewhat complicated by the fact that we must approximate all the system variables at any given grid point on the boundary, and we were not able to implement a stable termination for this network. The ``wave-canceling'' method [107] discussed in §3.11 becomes exceedingly complex when vector wave variables and reflection-free ports are involved; passivity is not easy to ensure.
Termination of the DWN derived from the MDKC of Figure 5.17, operating on the computational grid of Figure 5.18, however, is simpler, because we are able to work directly with the termination of the lumped mesh representation. Suppose we choose our southern boundary at ![]() according to Figure 5.19. The only quantities to be calculated in this arrangement will be
according to Figure 5.19. The only quantities to be calculated in this arrangement will be ![]() and
and
![]() , at coincident series scattering junctions, and
, at coincident series scattering junctions, and ![]() at parallel scattering junctions. This arrangement is to be preferred, because we do not need to worry about the termination of the vector scattering junctions at which
at parallel scattering junctions. This arrangement is to be preferred, because we do not need to worry about the termination of the vector scattering junctions at which
![]() is calculated.
is calculated.
The southern boundary terminations corresponding to the four conditions (5.44) are shown in Figure 5.20. The conditions ![]() and
and
![]() that appear in (5.44a) and (5.44d) can be dealt with rather simply, by terminating the boundary series junctions at which the junction currents
that appear in (5.44a) and (5.44d) can be dealt with rather simply, by terminating the boundary series junctions at which the junction currents ![]() and
and
![]() are calculated in an open circuit
are calculated in an open circuit![]() . For these conditions, the gyrator coupling between the two subnetworks (indicated by curved arrows in Figure 5.19) may be dropped entirely. Similarly, the condition
. For these conditions, the gyrator coupling between the two subnetworks (indicated by curved arrows in Figure 5.19) may be dropped entirely. Similarly, the condition
![]() can be implemented by short-circuiting the appropriate parallel boundary junctions.
can be implemented by short-circuiting the appropriate parallel boundary junctions.
The other conditions, involving variables not calculated directly on the boundary require a slightly more involved treatment; the analysis is similar to that performed in §4.4.4, and the termination problem becomes (for the most part) that of setting the self-loop immittances at the boundary junctions which can not be trivially terminated in an open or short circuit. To this end, we provide the waveguide immittances at the junctions in the problem interior at which ![]() ,
,
![]() and
and ![]() are calculated. From Figure 5.17, it is possible to read off these values directly. As for the DWN for the Timoshenko
system in §5.2.2, immittances in the two overlapped networks are distinguished by a tilde (
are calculated. From Figure 5.17, it is possible to read off these values directly. As for the DWN for the Timoshenko
system in §5.2.2, immittances in the two overlapped networks are distinguished by a tilde (
![]() ).
For example, at a parallel junction in the five-variable grid at location
).
For example, at a parallel junction in the five-variable grid at location
![]() ,
, ![]() , for
, for ![]() and
and ![]() integer, where we calculate
integer, where we calculate
![]() (see Figure 5.18), there are waveguide connections to the north, south, east and west; their admittances are defined as
(see Figure 5.18), there are waveguide connections to the north, south, east and west; their admittances are defined as