Note on Boundary Conditions

In the analysis above, the spatial domain is assumed unbounded (i.e., we took 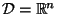$\mathcal{D} = \mathbb{R}^{n}$). It is useful to examine the energetic behavior of (3.1) if this is not the case. Integrating (3.3) over 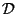$\mathcal{D}$, we get

$$\frac{d}{d t}\int_{\mathcal{D}}\frac{1}{2}\left({\bf w}^{T}{\bf P... ...dV + \frac{1}{2}\int_{\mathcal{D}}{\bf w}^{T}({\bf B}+{\bf B}^{T}){\bf w}dV = 0$$

where $\nabla\triangleq [\frac{\partial}{\partial x_{1}},\hdots,\frac{\partial}{\partial x_{n}}]^{T}$, and where we have defined

$${\bf b} \triangleq \frac{1}{2}[{\bf w}^{T}{\bf A}_{1}{\bf w},\hdots, {\bf w}^{T}{\bf A}_{n}{\bf w}]^{T}$$

If the boundary of 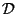$\mathcal{D}$ is sufficently smooth, then upon applying the Divergence Theorem, we get

$$\frac{d}{d t}\int_{\mathcal{D}}\frac{1}{2}\left({\bf w}^{T}{\bf P... ...igma+\frac{1}{2}\int_{\mathcal{D}}{\bf w}^{T}({\bf B}+{\bf B}^{T}){\bf w}dV = 0$$

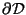where $\partial\mathcal{D}$ is the boundary of 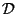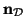$\mathcal{D}$, ${\bf n}_{\mathcal{D}}$ is defined as the unit outward normal (assumed unique everywhere on 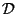$\mathcal{D}$ except over a set of measure zero), and 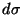$d\sigma$ is a surface element of 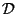$\mathcal{D}$. If we define the total energy by

$$E(t) \triangleq \int_{\mathcal{D}}\frac{1}{2}\left({\bf w}^{T}{\bf Pw}\right)dV$$

then we have

$$\frac{d}{dt}{E} = - \int_{\partial \mathcal{D}}{\bf b}^{T}{\bf n}... ...}d\sigma-\frac{1}{2}\int_{\mathcal{D}}{\bf w}^{T}({\bf B}+{\bf B}^{T}){\bf w}dV$$

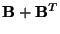If ${\bf B}+{\bf B}^{T}$ is positive semi-definite, then a simple condition for passivity is

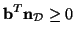$${\bf b}^{T}{\bf n}_{\mathcal{D}} \geq 0$$ (3.8)

and the system is lossless if 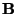${\bf B}$ is antisymmetric and (3.8) holds with equality.

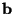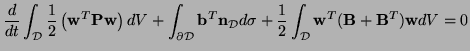
This analysis is grossly incomplete, however, because we have not said anything about which boundary conditions ensure the existence and uniqueness of a solution; this analysis is rather involved, and we refer the reader to [82] for an introduction. The basic issue is the over- or under-specification of ${\bf b}$ on the boundary. We will consider only lossless, memoryless boundary conditions in this thesis.