Free Edge

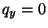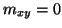Referring to Figure 5.20(a), the conditions $q_{y} = 0$ and $m_{xy} = 0$ are rather simply dealt with by open- or short-circuiting the respective junctions. In this case, the gyrator connection between the two waveguide meshes can be severed at the boundary junctions, and in order to get a lossless numerical condition equivalent to 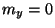$m_{y} = 0$ we need only set, for $j=0$,

$$\tilde{Z}_{c,i,0} = \frac{v_{0}(\rho h^{3})_{i,0}}{12}-r_{2}$$

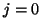which is less restrictive than (5.45b), and does not degrade the bound from (5.38) and (5.42).

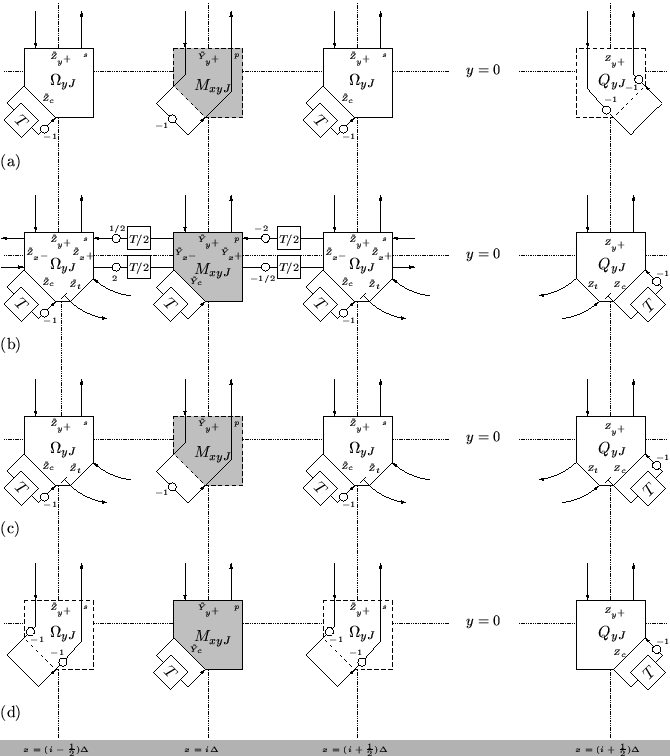
Figure 5.20: Various lossless boundary terminations for the DWN for Mindlin's system-- (a) free boundary; (b) simply supported edge (1); (c) simply supported edge (2); (d) clamped edge.