


Next: Grid Arrangement Requiring Voltage
Up: The (2+1)D Parallel-plate System
Previous: Reduced Computational Complexity and
Boundary Conditions
We now examine the termination of the waveguide mesh which simulates the behavior of the (2+1)D parallel-plate equations. The two most important types of boundary conditions are
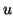 |
 |
|
Short-circuit termination |
(4.80) |
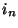 |
 |
|
Open-circuit termination |
(4.81) |
where 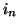 refers to the component of
refers to the component of
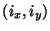 which is normal to the boundary. Condition (4.68) corresponds to a transmission line plate pair which are connected (and thus short-circuited) at the boundary; the same condition holds for a clamped membrane for which
which is normal to the boundary. Condition (4.68) corresponds to a transmission line plate pair which are connected (and thus short-circuited) at the boundary; the same condition holds for a clamped membrane for which 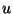 is interpreted as a transverse velocity, and
is interpreted as a transverse velocity, and
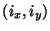 as in-plane forces. Condition (4.69) is an open-circuited termination; current can not leave the plate at the edges. This second condition is analogous to the rigid termination of a (2+1)D acoustic medium, where
as in-plane forces. Condition (4.69) is an open-circuited termination; current can not leave the plate at the edges. This second condition is analogous to the rigid termination of a (2+1)D acoustic medium, where
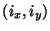 are interpreted as flow velocities, and
are interpreted as flow velocities, and 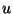 as a pressure. Both conditions are of the form of (3.8), and are lossless. We will examine only the termination of the mesh on a rectangular domain (though the result extends easily to the radial mesh to be discussed in §4.6.2).
as a pressure. Both conditions are of the form of (3.8), and are lossless. We will examine only the termination of the mesh on a rectangular domain (though the result extends easily to the radial mesh to be discussed in §4.6.2).
In the case of the (1+1)D transmission line, we could treat a staggered mesh terminated by a parallel junction, and through the duality of  and
and 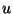 extend the result to include termination by a series junction (see §4.3.9). This is no longer the case in (2+1)D, and we must treat the two types of termination separately. Consider a bottom (southern) boundary at
extend the result to include termination by a series junction (see §4.3.9). This is no longer the case in (2+1)D, and we must treat the two types of termination separately. Consider a bottom (southern) boundary at 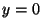 of an interleaved mesh of the type shown in Figure 4.21. The two possible types of termination are shown in Figure 4.23.
of an interleaved mesh of the type shown in Figure 4.21. The two possible types of termination are shown in Figure 4.23.
Figure 4.23:
Grid terminations at a southern boundary.
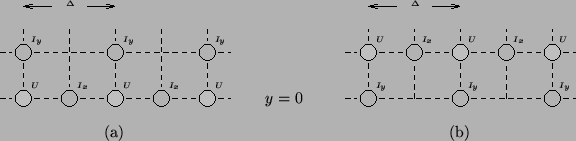 |
Subsections



Next: Grid Arrangement Requiring Voltage
Up: The (2+1)D Parallel-plate System
Previous: Reduced Computational Complexity and
Stefan Bilbao
2002-01-22
![]() and
and ![]() extend the result to include termination by a series junction (see §4.3.9). This is no longer the case in (2+1)D, and we must treat the two types of termination separately. Consider a bottom (southern) boundary at
extend the result to include termination by a series junction (see §4.3.9). This is no longer the case in (2+1)D, and we must treat the two types of termination separately. Consider a bottom (southern) boundary at ![]() of an interleaved mesh of the type shown in Figure 4.21. The two possible types of termination are shown in Figure 4.23.
of an interleaved mesh of the type shown in Figure 4.21. The two possible types of termination are shown in Figure 4.23.