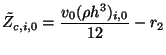Simply Supported Edge (2)

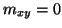The condition $m_{xy} = 0$ from (5.44c) can be set by short-circuiting the parallel boundary junctions. The condition 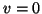$v=0$ can be dealt with as for the preceding case, and we will again require

$$Z_{c,i,0} = \frac{v_{0}}{(\kappa^{2}Gh)_{i,0}}-r_{1}$$

and the gyrator coefficient at the boundary junctions should be set to 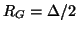$R_{G} = \Delta/2$. The self-loop impedances at the series junctions in the five-variable mesh should be set, in order to ensure 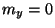$m_{y} = 0$, as

$$\tilde{Z}_{c,i,0} = \frac{v_{0}(\rho h^{3})_{i,0}}{12}-r_{2}$$

The positivity requirement on this impedance is again less restrictive than condition (5.45b) on the mesh interior.