Incorporating the DWN into the MDWD Framework

At this point, the reader may have noticed more than a few similarities between the treatment of transmission lines in this chapter and the last. It should be recalled from Chapter 3 that the multidimensional wave digital networks that numerically integrate the parallel-plate system are derived from multidimensional Kirchoff circuits under a set of coordinate transformations and spectral mappings from the continuous to discrete domain. A DWN, on the other hand, is constructed entirely in the discrete time and space domain, and is then identified with a finite difference method consistent with the problem.

It will be shown in this section that certain DWNs may in fact be derived from an MDKC under an alternative spectral mapping (also passivity-preserving), provided new wave digital circuit elements (multidimensional unit elements) are also defined. In this way, the DWN may be considered to be a multidimensional wave digital network in its own right, depending on how attached one feels to the trapezoid rule as an integration method. The behavior of TLM and wave-digital numerical integration methods have been previously compared in [131] and [71], and the material in this section also appears in [18].

It is instructive to first reconsider the (1+1)D transmission line system in the lossless source-free case. In Figure 4.44 are presented both the type III DWN, and the MDWD network for the same system using offset sampling, with spatial dependence expanded out. For the MDWD network, we have chosen a grid spacing of $\Delta/2$, and a time step of $T/2$ so as to align it with the DWN. (In other words, we have used $T_{1} = T_{2} = \Delta/\sqrt{2}$-- see §3.7 for details.)

Figure 4.44: Signal flow diagrams of the DWN and MDWD networks for the (1+1)D lossless source-free transmission line.

First, notice that for the DWN, we have one three-port scattering junction at each grid point, and that parallel junctions are interleaved with series junctions. Approximations to $i$ and $u$ are calculated at alternating grid points, and at alternating multiples of the time step, $T/2$. For the MDWDF, we have two two-port series adaptors at each grid point; we are approximating both $i$ and $u$ together at the same locations, though due to offset sampling, these locations alternate from one time step to the next. Both variables are treated as currents. For both networks, all the material variation of the transmission line is expressed in the immittances of self-loops at every junction or adaptor, the delay in which is twice that of the linking delay between adjacent grid points. It is also useful to compare the waveguide immittances to the port resistances of the MDWDF. We have

$$R_{1} = \frac{2}{\Delta}\left(v_{0}l-r_{0}\right)\hspace{0.3in}R_... ...}\left(v_{0}r_{0}^{2}c-r_{0}\right)\hspace{0.3in} R_{0} = \frac{4r_{0}}{\Delta}$$

and

$$Z_{c} = 2\left(v_{0}l-r_{0}\right)\hspace{0.3in}Y_{c} = 2\left(v_... ...0.3in}Z_{x^{-}} = Z_{x^{+}} = \frac{1}{Y_{x^{-}}} = \frac{1}{Y_{x^{+}}} = r_{0}$$

where we recall, from the discussion of the type III waveguide network in §4.3.6, that the connecting impedances were chosen to be some constant $Z_{const}$, in this case $Z_{const} = r_{0}$.

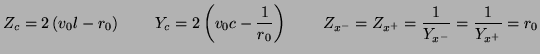Enforcing the positivity of $R_{1}$ and $R_{2}$ or $Z_{c}$ and $Y_{c}$ leads to identical stability conditions, and the self-loop immittances and inductances are simply related to one another by

$$Z_{c} = \Delta R_{1}\hspace{0.3in}Y_{c} = \Delta R_{2}/r_{0}^{2}$$

at locations for which both quantities coexist in their respective discrete networks.

Most important, though, is the observation that, whereas the DWN can be considered to be made up of an array of lumped two-port bidirectional delay lines, the signal flow diagram of the MDWD network in Figure 4.44 does not have such an interpretation--the port in this setting is defined only as a multidimensional object, and instances of this port in the discrete domain are not connected port-wise. It is crucial to recognize that passivity of such a discrete network is reflected by the power conservation of the scattering operation, and not by where wave variables go in the network after they have been scattered; in particular, they need not be paired as they are for waveguide networks, as long as the shifting operation which they undergo subsequently does not increase energy in the network. On the other hand, as we shall see in Chapter 5, boundary conditions are much easier to implement in a lumped network.