


Next: Hybrid Form of the
Up: Incorporating the DWN into
Previous: Incorporating the DWN into
As a first step towards reintroducing this port structure to a MDWD network (and hence towards relating the DWN to the MDWDF), we can extend the definition of the unit element (and recall from §4.2.1 that the unit element is a wave digital two-port which is equivalent to a single bidirectional delay line) to multi-D in the following way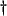 . Suppose that we are dealing with a (1+1)D system, and new coordinates
. Suppose that we are dealing with a (1+1)D system, and new coordinates 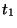 and
and 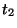 are as defined by (3.18). We thus have two transform frequencies
are as defined by (3.18). We thus have two transform frequencies 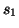 and
and 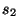 , as well as two frequency-domain shift-operators
, as well as two frequency-domain shift-operators
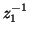 and
and
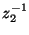 in the two directions
in the two directions 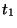 and
and 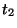 . The multidimensional two-port defined, at steady-state, by
. The multidimensional two-port defined, at steady-state, by
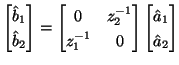 |
(4.121) |
and shown in Figure 4.45(a) bears some resemblance to the lumped unit element discussed initially in §2.3.4; it is clearly lossless (because it merely implements a pair of shifts), but, unlike the unit element, it is no longer reciprocal. In this last respect, we remark that a multidimensional element so defined is perhaps closer in spirit to a generalization of the so-called quasi-reciprocal line (QUARL) proposed by Fettweis [46]. The two port resistances are assumed identical and equal to some positive constant 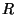 . When the spatial dependence is expanded out, it appears as an entire array of unit elements, as in Figure 4.45(b), where we have assumed
. When the spatial dependence is expanded out, it appears as an entire array of unit elements, as in Figure 4.45(b), where we have assumed
where
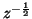 and
and
 correspond, respectively, to unit shifts in time and space by
correspond, respectively, to unit shifts in time and space by 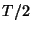 and
and 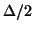 . We have thus chosen
. We have thus chosen
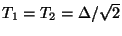 .
.
Figure 4.45: (a) Multidimensional unit element at steady state making use of shifts in directions 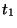 and
and 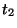 and (b) its steady state schematic when spatial dependence is expanded out.
and (b) its steady state schematic when spatial dependence is expanded out.
 |
This element, like the standard unit element, is defined in the discrete (time and space) domain, and using wave variables. Rewriting the scattering relation in terms of steady-state discrete voltage and current amplitudes, (4.104) becomes the impedance relationship
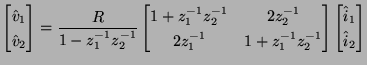 |
(4.122) |



Next: Hybrid Form of the
Up: Incorporating the DWN into
Previous: Incorporating the DWN into
Stefan Bilbao
2002-01-22
![]() . Suppose that we are dealing with a (1+1)D system, and new coordinates
. Suppose that we are dealing with a (1+1)D system, and new coordinates ![]() and
and ![]() are as defined by (3.18). We thus have two transform frequencies
are as defined by (3.18). We thus have two transform frequencies ![]() and
and ![]() , as well as two frequency-domain shift-operators
, as well as two frequency-domain shift-operators
![]() and
and
![]() in the two directions
in the two directions ![]() and
and ![]() . The multidimensional two-port defined, at steady-state, by
. The multidimensional two-port defined, at steady-state, by
