The Bidirectional Delay Line

The basic element in a waveguide network, and the one which does the work of moving energy from one part of the network to another, is the bidirectional delay line, shown in Figure 4.1.

Figure 4.1: Bidirectional delay line.

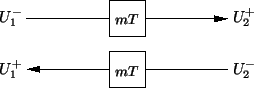It is no more than a pair of digital delay lines, whose delays are equal length (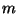$m$ samples of duration 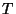$T$ in Figure 4.1). It should be understood that, for realizability, all delay lengths in a given network should be multiples of a common smallest (``unit'') delay. We will use the terms waveguide and bidirectional delay line interchangeably in this work.

Associated with the bidirectional delay line are two sets of signals, called waves: voltage waves 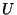$U$, and current waves $I$. Only voltage waves are shown in Figure 4.1. Waves of either type are indexed with respect to a particular end of the delay line; in Figure 4.1, waves at the left end of the delay line pair are subscripted with a ``1'', and those at the right end with a ``2''. In addition, one of the waves at either end enters the waveguide, and one leaves; the waves are superscripted with $-$ or 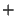$+$ respectively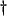. We can immediately read the relationship among the variables from Figure 4.1:

$$U_{2}^{+}(n) = U_{1}^{-}(n-m)\hspace{0.5in}U_{1}^{+}(n) = U_{2}^{-}(n-m)$$ (4.1)

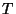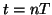The delay duration $T$ is implicit, so that a wave variable indexed by $n$ refers to the value of that quantity at time $t = nT$. In terms of 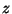$z$-transformed quantities [133] (which we will denote with a hat),

$$\hat{U}_{2}^{+} = z^{-m}\hat{U}_{1}^{-}\hspace{1.0in}\hat{U}_{1}^{+} = z^{-m}\hat{U}_{2}^{-}$$ (4.2)

We also define, at either end of the waveguide, the so-called physical voltage by

$$U_{j} = U_{j}^{+}+U_{j}^{-}\hspace{1.0in}j=1,2$$ (4.3)