Impedance

From the point of view of a programmer, the above description of the operation of an isolated bidirectional delay line is complete. In order to connect one bidirectional delay line to others, however, we must introduce the impedance 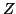$Z$, a positive number associated with a particular waveguide. The impedance allows us to define the relationship between the voltage waves and the current waves which were mentioned in the last section, which is:

$$\begin{eqnarray}U_{j}^{+} &=& \quad\! ZI_{j}^{+}\\ U_{j}^{-} &=& -ZI_{j}^{-} \end{eqnarray}$$ (4.4a)

where 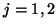$j=1,2$ referring to Figure 4.1, which implies, from (4.1), that we have

$$I_{2}^{+}(n) = -I_{1}^{-}(n-m)\hspace{0.5in}I_{1}^{+}(n) = -I_{2}^{-}(n-m)$$ (4.5)

Thus current waves entering a bidirectional delay line are delayed by the same amount as their voltage wave counterparts, but with sign inversion. In view of (4.4), we need only propagate a particular type of wave (i.e., either voltage or current) in a particular waveguide. In a waveguide network, however, we are free to use different types of waves in different waveguides, converting between the different types with (4.4) where necessary.

The admittance $Y$ of the waveguide is defined by

$$Y = \frac{1}{Z}$$

and we define the physical current at either end of the waveguide, like the voltage, to be the sum of the wave components. Thus we have

$$I_{j} = I_{j}^{+}+I_{j}^{-}\hspace{1.0in}j=1,2$$ (4.6)