Next: Note on the Different
Up: Digital Waveguides
Previous: Impedance
Wave Equation Interpretation
The second-order PDE describing the voltage distribution 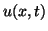 along an electrical transmission line with constant inductance and capacitance
along an electrical transmission line with constant inductance and capacitance  and
and  per unit length and which runs parallel to the
per unit length and which runs parallel to the  -axis is
-axis is
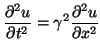 |
(4.7) |
where the wave speed 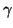 is
is
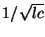 . As we saw in §1.1.1, the solution to this equation, if we set aside boundary conditions for the moment, can be written in terms of traveling waves:
. As we saw in §1.1.1, the solution to this equation, if we set aside boundary conditions for the moment, can be written in terms of traveling waves:
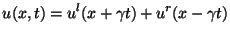 |
(4.8) |
That is, the solution at any time  is made up of a sum of two shifted copies of the initializing functions
is made up of a sum of two shifted copies of the initializing functions 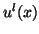 and
and 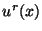 , which have traveled to the left and right respectively with velocity
, which have traveled to the left and right respectively with velocity 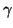 over a distance
over a distance 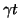 . For any
. For any  we have, for the leftward-traveling wave, the identity
we have, for the leftward-traveling wave, the identity
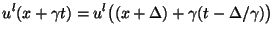 |
(4.9) |
If we set
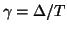 , then at time
, then at time 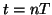 ,
,
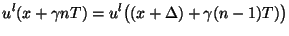 |
(4.10) |
Associate now with a particular waveguide a delay 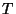 and a physical length
and a physical length  , so that in Figure 4.1
, so that in Figure 4.1 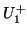 represents an outgoing voltage wave quantity at position
represents an outgoing voltage wave quantity at position  , and
, and 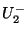 an incoming wave at position
an incoming wave at position 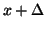 . It is then clear that if we have
. It is then clear that if we have
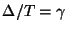 , then (4.10) is equivalent to the second equation of (4.1), with
, then (4.10) is equivalent to the second equation of (4.1), with 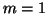 , and with
, and with
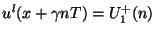 and
and
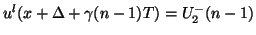 . A similar correspondence holds for the right-going traveling wave component
. A similar correspondence holds for the right-going traveling wave component 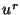 and the wave variables at either end of the rightward waveguide,
and the wave variables at either end of the rightward waveguide, 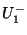 and
and 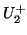 . A chain of bidirectional delay lines, connected in cascade will then implement an exact traveling wave solution to the wave equation. The physical voltage
. A chain of bidirectional delay lines, connected in cascade will then implement an exact traveling wave solution to the wave equation. The physical voltage 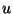 may be obtained (as should be clear from (4.8)) by summing the leftward and rightward traveling components at any particular location in the cascade, as per equation (4.3). Note that because
may be obtained (as should be clear from (4.8)) by summing the leftward and rightward traveling components at any particular location in the cascade, as per equation (4.3). Note that because
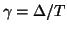 , the delay period and the waveguide length cannot be chosen independently, if the discrete wave quantities are to behave as traveling wave solutions to (4.7).
, the delay period and the waveguide length cannot be chosen independently, if the discrete wave quantities are to behave as traveling wave solutions to (4.7).



Next: Note on the Different
Up: Digital Waveguides
Previous: Impedance
Stefan Bilbao
2002-01-22