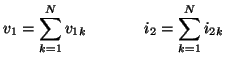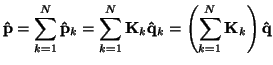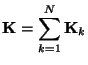Next: Alternative MDKC for the
Up: Incorporating the DWN into
Previous: Multidimensional Unit Elements
Hybrid Form of the Multidimensional Unit Element
We now have an impedance relationship describing the multidimensional unit element in terms of the discrete frequency variables
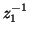 and
and
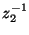 . It is of interest, however, to introduce a particular type of hybrid form [12]. The reason for doing this ultimately has to do with the fact that in a DWN in interleaved form, such as that shown in Figure 4.14 or 4.21, a typical linking waveguide (or unit element) is connected in parallel at one port and in series at the other; it is somewhat easier to make the transition from wave digital filters to digital waveguide networks if we take account of this asymmetry.
. It is of interest, however, to introduce a particular type of hybrid form [12]. The reason for doing this ultimately has to do with the fact that in a DWN in interleaved form, such as that shown in Figure 4.14 or 4.21, a typical linking waveguide (or unit element) is connected in parallel at one port and in series at the other; it is somewhat easier to make the transition from wave digital filters to digital waveguide networks if we take account of this asymmetry.
Suppose we have a two-port which is defined, at steady-state, by the relationship
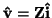 , or
, or
This can be rewritten in a so-called hybrid form as
or as
For the multidimensional unit element defined by (4.104), the hybrid matrix is, given the impedance relation (4.105),
It should be clear that the definition of the unit element holds regardless of which complex frequencies we choose. In particular, the delays
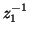 and
and
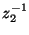 could be replaced by delays in higher dimensional spaces (we will make use of this in §4.10.4, §4.10.5 and §4.10.6). We will enforce the order of the arguments of
could be replaced by delays in higher dimensional spaces (we will make use of this in §4.10.4, §4.10.5 and §4.10.6). We will enforce the order of the arguments of
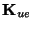 so that, for example,
so that, for example,
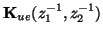 and
and
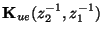 refer to unit elements of mirror-image orientation.
refer to unit elements of mirror-image orientation.
Suppose now that we have  two-ports defined by their impedance and hybrid relationships
two-ports defined by their impedance and hybrid relationships
Figure:
Series/parallel connection of  two-ports.
two-ports.
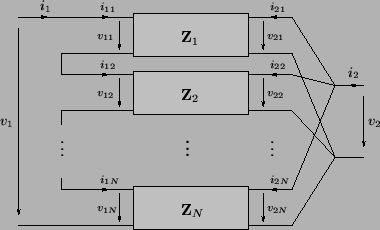 |
If we are interested in connecting the first ports of all  two-ports to each other in series, and the second ports in parallel as in Figure 4.46, then we will have, for the total voltages and currents
two-ports to each other in series, and the second ports in parallel as in Figure 4.46, then we will have, for the total voltages and currents
and
which hold instantaneously, and thus, in order to describe the two-port resulting from the connection, we may write
Thus for such a series/parallel combination of two-ports, the hybrid matrix of the connection is simply the sum of the hybrid matrices of the individual two-ports, and thus



Next: Alternative MDKC for the
Up: Incorporating the DWN into
Previous: Multidimensional Unit Elements
Stefan Bilbao
2002-01-22
![]() , or
, or
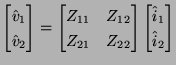
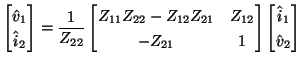
![]() two-ports defined by their impedance and hybrid relationships
two-ports defined by their impedance and hybrid relationships