


Next: Scattering Networks for Maxwell's
Up: Maxwell's Equations
Previous: Maxwell's Equations
If 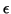 and
and  are constant, then from (3.10), the dispersion relation for Maxwell's Equations has the form
are constant, then from (3.10), the dispersion relation for Maxwell's Equations has the form
in terms of frequencies 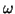 and wavenumber magnitudes
and wavenumber magnitudes

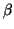
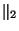 . This equation has solutions
. This equation has solutions
Leaving aside the non-propagating mode with
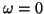 , the phase and group velocities will then be given by
, the phase and group velocities will then be given by
For spatially inhomogeneous problems, the maximum group velocity will be
Stefan Bilbao
2002-01-22
![]() and
and ![]() are constant, then from (3.10), the dispersion relation for Maxwell's Equations has the form
are constant, then from (3.10), the dispersion relation for Maxwell's Equations has the form
