The (1+1)D Advection Equation

Perhaps the simplest hyperbolic partial differential equation imaginable is the so-called scalar advection or one-way wave equation in (1+1)D, defined by

$$\frac{\partial i}{\partial t}+\alpha\frac{\partial i}{\partial x}=0$$ (3.47)

where 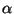$\alpha$ is a real constant [176]. It is complemented by the initial condition

$$i(x,0) = i_{0}(x),\hspace{1.0in} -\infty<x<\infty$$ (3.48)

Here, the solution 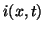$i(x,t)$ is assumed continuously differentiable (though it need not be), and is defined over the entire $x$-axis, and for $t\geq 0$. The solution is simply

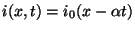$$i(x,t) = i_{0}(x-\alpha t)$$ (3.49)

That is, the initial data travels to the left or right (depending on the sign of 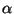$\alpha$) with speed 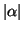$\vert\alpha\vert$. Despite its simplicity, it is often used as a model for numerical schemes [95].