


Next: The (1+1)D Advection Equation
Up: MD Circuit Elements
Previous: Discretization in the Spectral
Other Spectral Mappings
One could well ask whether the spectral mappings of the form (3.43), which correspond to an application of the trapezoid rule, are the only means of deriving an MD-passive discrete system from a continuous one. The criterion for a passivity-preserving mapping is that it map multidimensional positive real functions (i.e., functions whose real parts are positive when the real parts of all of their arguments are positive) to functions which have the same property in a generalized multidimensional outer disk.
In a brief section of one of the original papers on the subject of WD integration [61], a different type of mapping is proposed, in a discussion of boundary conditions for the transmission line equations. Suppose that, in the (1+1)D case, our transformed coordinates are given by (3.18). The alternative mapping can be written as
where the frequency variables  and
and  are defined in terms of the variables
are defined in terms of the variables 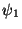 and
and 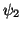 from (3.43) by
from (3.43) by
 |
(3.45a) |
We then have that
from which we can conclude that
Another simple way of seeing positive realness is by rewriting (3.49) as
 |
(3.46a) |
in which case  and
and  can be viewed as impedances of parallel combinations of passive (indeed, lossless) elements. For example,
can be viewed as impedances of parallel combinations of passive (indeed, lossless) elements. For example,  is equivalent to the impedance of a parallel combination of an inductor of impedance
is equivalent to the impedance of a parallel combination of an inductor of impedance 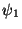 and a capacitor of impedance
and a capacitor of impedance
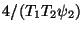 . Second-order accuracy is also obtained under these mappings; this should be clear from (3.50) as well.
This spectral mapping differs from the trapezoid rule in that the discrete spectral images of the two continuous frequency variables
. Second-order accuracy is also obtained under these mappings; this should be clear from (3.50) as well.
This spectral mapping differs from the trapezoid rule in that the discrete spectral images of the two continuous frequency variables 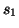 and
and 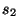 are now mixtures of the two discrete frequency variables
are now mixtures of the two discrete frequency variables
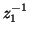 and
and
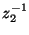 . In addition, the transformation does not have a unique inverse, but this is of little consequence because we will never have any occasion to invert such a mapping. We mention this particular mapping, because it will serve as the bridge between multidimensional wave digital filters and digital waveguide networks (to be discussed in Chapter 4). We will spend some time in §4.10 elaborating this link. It will also allow us to introduce higher-order accurate methods, which we will discuss in §3.13.
. In addition, the transformation does not have a unique inverse, but this is of little consequence because we will never have any occasion to invert such a mapping. We mention this particular mapping, because it will serve as the bridge between multidimensional wave digital filters and digital waveguide networks (to be discussed in Chapter 4). We will spend some time in §4.10 elaborating this link. It will also allow us to introduce higher-order accurate methods, which we will discuss in §3.13.



Next: The (1+1)D Advection Equation
Up: MD Circuit Elements
Previous: Discretization in the Spectral
Stefan Bilbao
2002-01-22
