


Next: Other Spectral Mappings
Up: MD Circuit Elements
Previous: Other MD Elements
Discretization in the Spectral Domain
If our network or  -port is linear and shift-invariant, it is also possible to view the discretization procedure as a spectral mapping, just as in the last chapter. Consider now the case where the problem domain is some
-port is linear and shift-invariant, it is also possible to view the discretization procedure as a spectral mapping, just as in the last chapter. Consider now the case where the problem domain is some  -dimensional space, with coordinates
-dimensional space, with coordinates
![$ \mathbf{u}=[x_{1},\hdots,x_{n},t]^{T}$](img539.png) , and where we have changed coordinates to
, and where we have changed coordinates to
![$ \mathbf{t}=[t_{1},\hdots, t_{k}]^{T}$](img692.png) , with
, with 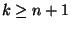 via a transformation of type (3.21). The defining equation of an MD inductor of direction
via a transformation of type (3.21). The defining equation of an MD inductor of direction 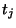 for any
for any
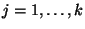 is
is
and for an exponential state at frequencies
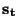 , we have
, we have
where
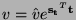 and
and
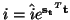 . The ``impedance'' is here
. The ``impedance'' is here
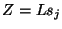 and clearly satisfies MD positive realness criterion given in (3.31) (and furthermore is MD-lossless) if
and clearly satisfies MD positive realness criterion given in (3.31) (and furthermore is MD-lossless) if 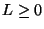 . As in the lumped case, the trapezoid rule, now applied in the
. As in the lumped case, the trapezoid rule, now applied in the 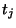 direction, can be interpreted as a spectral mapping
direction, can be interpreted as a spectral mapping
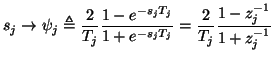 |
(3.42) |
where 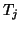 is some arbitrary step-size in the
is some arbitrary step-size in the 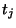 direction. For notational purposes, we have used
direction. For notational purposes, we have used
to represent the frequency domain equivalent of a unit shift in the 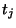 direction. In complete analogy with the lumped case, (3.43) implies that
direction. In complete analogy with the lumped case, (3.43) implies that
This shift can of course also be written in terms of delays and shifts in the
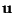 coordinates. For example, consider the coordinate transformation defined in (3.18). In this case we have, in the frequency domain,
coordinates. For example, consider the coordinate transformation defined in (3.18). In this case we have, in the frequency domain,
where 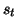 and
and 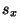 are the frequency variables conjugate to
are the frequency variables conjugate to 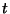 and
and  respectively. (We assume that our spatial domain is of infinite extent, so that
respectively. (We assume that our spatial domain is of infinite extent, so that 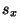 corresponds to an imaginary Fourier transform variable.) Suppose we have also chosen the step-sizes in the two coordinates such that the grids overlap, that is,
corresponds to an imaginary Fourier transform variable.) Suppose we have also chosen the step-sizes in the two coordinates such that the grids overlap, that is,
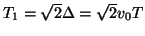 , where
, where 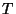 is the shift in the pure time direction. Then, for a shift of
is the shift in the pure time direction. Then, for a shift of 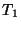 in the
in the 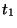 direction, we can write
direction, we can write
or
 |
(3.43) |
where 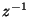 represents a delay of duration
represents a delay of duration 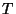 in the time direction, and
in the time direction, and 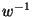 corresponds to a shift over distance
corresponds to a shift over distance  in the positive space direction. Similarly, we can write
in the positive space direction. Similarly, we can write
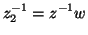 |
(3.44) |
For a more complex example, consider again the transformation defined by
which maps coordinates
![$ [x,y,t]^{T}$](img712.png) to a five-dimensional coordinates
to a five-dimensional coordinates
![$ [t_{1},t_{2},t_{3},t_{4},t_{5}]^{T}$](img713.png) . A shift of
. A shift of
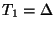 in direction
in direction 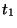 corresponds to a transmittance of the form
corresponds to a transmittance of the form
where 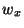 represents a unit shift (of length
represents a unit shift (of length  ) in the
) in the  -direction, and as before,
-direction, and as before, 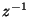 corresponds to a unit delay of
corresponds to a unit delay of
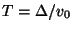 . The other shifts can be written as
. The other shifts can be written as
where 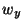 represents a unit shift (of length
represents a unit shift (of length  ) in the
) in the 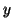 direction.
At a given grid point in the old coordinates, the unit delays
direction.
At a given grid point in the old coordinates, the unit delays
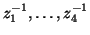 , interpreted as directional shifts, refer to points on the grid at the previous time step, and located one grid point away in the
, interpreted as directional shifts, refer to points on the grid at the previous time step, and located one grid point away in the 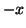 ,
, 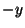 ,
,  and
and 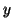 directions, respectively. The unit delay
directions, respectively. The unit delay
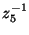 is simply a unit time delay.
is simply a unit time delay.
It is important to note the manner in which the special character of the coordinate transformation manifests itself here. Due to the positivity requirement on the elements of the last column of
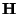 , a unit delay in any of the directions
, a unit delay in any of the directions 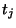 will always include some delay in the pure time direction. By means of this requirement, and the introduction of wave variables, MDWD networks can, in the same way as their lumped counterparts, be designed in which delay-free loops do not appear. Such networks, when used for simulation, will give rise, in general, to explicit numerical schemes [176].
will always include some delay in the pure time direction. By means of this requirement, and the introduction of wave variables, MDWD networks can, in the same way as their lumped counterparts, be designed in which delay-free loops do not appear. Such networks, when used for simulation, will give rise, in general, to explicit numerical schemes [176].



Next: Other Spectral Mappings
Up: MD Circuit Elements
Previous: Other MD Elements
Stefan Bilbao
2002-01-22
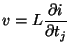
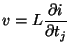
![]() coordinates. For example, consider the coordinate transformation defined in (3.18). In this case we have, in the frequency domain,
coordinates. For example, consider the coordinate transformation defined in (3.18). In this case we have, in the frequency domain,
![]() and
and ![]() are the frequency variables conjugate to
are the frequency variables conjugate to ![]() and
and ![]() respectively. (We assume that our spatial domain is of infinite extent, so that
respectively. (We assume that our spatial domain is of infinite extent, so that ![]() corresponds to an imaginary Fourier transform variable.) Suppose we have also chosen the step-sizes in the two coordinates such that the grids overlap, that is,
corresponds to an imaginary Fourier transform variable.) Suppose we have also chosen the step-sizes in the two coordinates such that the grids overlap, that is,
![]() , where
, where ![]() is the shift in the pure time direction. Then, for a shift of
is the shift in the pure time direction. Then, for a shift of ![]() in the
in the ![]() direction, we can write
direction, we can write
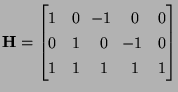
![]() , a unit delay in any of the directions
, a unit delay in any of the directions ![]() will always include some delay in the pure time direction. By means of this requirement, and the introduction of wave variables, MDWD networks can, in the same way as their lumped counterparts, be designed in which delay-free loops do not appear. Such networks, when used for simulation, will give rise, in general, to explicit numerical schemes [176].
will always include some delay in the pure time direction. By means of this requirement, and the introduction of wave variables, MDWD networks can, in the same way as their lumped counterparts, be designed in which delay-free loops do not appear. Such networks, when used for simulation, will give rise, in general, to explicit numerical schemes [176].