It is easy to see that the MDKC of Figure 3.6(a) will be MD-passive if the inductances ![]() and
and ![]() , and consequently the port resistances
, and consequently the port resistances ![]() and
and ![]() of the MDWDF in Figure 3.6(b) are non-negative. From (3.54), this gives a constraint on
of the MDWDF in Figure 3.6(b) are non-negative. From (3.54), this gives a constraint on ![]() , the space step/time step ratio, namely that we must have
, the space step/time step ratio, namely that we must have
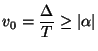 (for passivity) (for passivity) |
It is important to mention, however, that the instances of the MDWDF, sampled at every grid point as in Figure 3.7 are not connected port-wise, as must be true for a traditional lumped WD-network. The output wave at the bottom port at spatial location
![]() is sign-inverted and then sent as input to the same port, at location
is sign-inverted and then sent as input to the same port, at location
![]() at the next time step. Thus the realization of Figure 3.7 can not be analyzed directly as a chain of lumped elements; passivity follows from the multidimensional representations shown in Figure 3.6.
at the next time step. Thus the realization of Figure 3.7 can not be analyzed directly as a chain of lumped elements; passivity follows from the multidimensional representations shown in Figure 3.6.