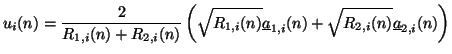Next: The Gas Dynamics Equations
Up: Applications in Fluid Dynamics
Previous: Nonlinear Circuit Elements
A simple nonlinear PDE which is often used as a model problem for fluid dynamical systems is given by the inviscid Burger's equation [82]:
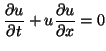 |
(B.4) |
It is similar in form to the advection equation mentioned in §3.6, and as we will see, its circuit representation is identical. The problem is assumed to be defined for
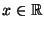 ,
,  .
. 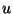 can be considered to be a current, as before, through a single loop, and Kirchoff's Voltage Law around the loop will give (B.4). The question however, is of the type of circuit elements to be included in this loop; clearly they must be nonlinear, and certainly reactive as well. We note that the viscous form of Burger's equation was approached in this way in [202].
can be considered to be a current, as before, through a single loop, and Kirchoff's Voltage Law around the loop will give (B.4). The question however, is of the type of circuit elements to be included in this loop; clearly they must be nonlinear, and certainly reactive as well. We note that the viscous form of Burger's equation was approached in this way in [202].
Using coordinate transformation (3.18), (B.4) can be rewritten as
Assuming that the solution is differentiable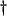 , this can be rewritten as
, this can be rewritten as
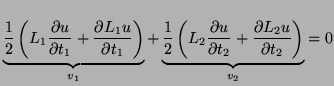 |
(B.5) |
where
 |
(B.6) |
Thus Burger's equation, in the form of (B.5), can be interpreted as a series combination of two nonlinear inductances, as shown in Figure B.1(a). The resultant MDWD network, with port resistances
 |
(B.7) |
appears in Figure B.1(b). We emphasize that this network is passive only if power-normalized wave variables are employed.
Figure B.1:
The (1+1)D inviscid Burger's equation-- (a) MDKC and (b) MDWD network.
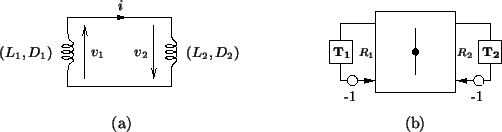 |
The positivity condition on these inductances now depends on the solution itself, 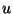 , and we must have
, and we must have
An a priori estimate of
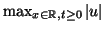 must be available; this is a consistent feature of all the circuit-based methods (and, it would seem, any explicit method) for the fluids systems that we will examine presently.
must be available; this is a consistent feature of all the circuit-based methods (and, it would seem, any explicit method) for the fluids systems that we will examine presently.
Let us now examine the scattering operation. First choose
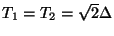 , so that the current grid function for the current at location
, so that the current grid function for the current at location 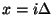 and
and 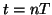 can be written as
can be written as 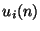 . The two power-normalized input wave variables entering the adaptor at the same location and time step are
. The two power-normalized input wave variables entering the adaptor at the same location and time step are
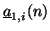
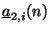 , and we have
, and we have
which, from (B.6) and (B.7), and using
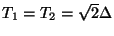 and
and
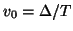 can be rewritten as
can be rewritten as
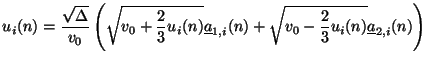 |
(B.8) |
This is precisely the nonlinear algebraic equation which is to be solved (in 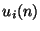 ); once
); once 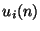 is determined, then so are the port resistances, and the output wave variables
is determined, then so are the port resistances, and the output wave variables
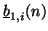 and
and
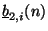 can be obtained through scattering as per (2.33). As mentioned before, it is not at all clear from the form of (B.8) whether a solution exists and is unique. We note, however, that we (and others [16,70]) have successfully programmed simulations for the gas dynamics equations (see next section), using simple iterative methods to solve the nonlinear algebraic systems; the results would appear to be in accord with published simulation results using differencing methods [171].
can be obtained through scattering as per (2.33). As mentioned before, it is not at all clear from the form of (B.8) whether a solution exists and is unique. We note, however, that we (and others [16,70]) have successfully programmed simulations for the gas dynamics equations (see next section), using simple iterative methods to solve the nonlinear algebraic systems; the results would appear to be in accord with published simulation results using differencing methods [171].



Next: The Gas Dynamics Equations
Up: Applications in Fluid Dynamics
Previous: Nonlinear Circuit Elements
Stefan Bilbao
2002-01-22
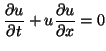
![]() ,
, ![]() .
. ![]() can be considered to be a current, as before, through a single loop, and Kirchoff's Voltage Law around the loop will give (B.4). The question however, is of the type of circuit elements to be included in this loop; clearly they must be nonlinear, and certainly reactive as well. We note that the viscous form of Burger's equation was approached in this way in [202].
can be considered to be a current, as before, through a single loop, and Kirchoff's Voltage Law around the loop will give (B.4). The question however, is of the type of circuit elements to be included in this loop; clearly they must be nonlinear, and certainly reactive as well. We note that the viscous form of Burger's equation was approached in this way in [202].
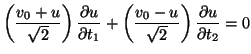
![]() , so that the current grid function for the current at location
, so that the current grid function for the current at location ![]() and
and ![]() can be written as
can be written as ![]() . The two power-normalized input wave variables entering the adaptor at the same location and time step are
. The two power-normalized input wave variables entering the adaptor at the same location and time step are
![]()
![]() , and we have
, and we have