|
Chapter 4, which is concerned with digital waveguide networks, is rather large, and can be conveniently divided into three principal parts.
The first part of the chapter, from §4.1 to §4.5, deals with the relationship between digital waveguide networks and finite difference methods of the FDTD variety; we showed a very simple example of such a correspondence in §1.1.2. We reintroduce digital waveguide networks, now in the electrical context, so as to make easier the eventual comparison with the wave digital networks of Chapters 2 and 3--the acoustic tubes in the Kelly-Lochbaum model of §1.1.1 and the waveguide mesh of §1.1.2 are thus replaced by transmission line sections, and pressures and velocities become voltages and currents. After a brief review of the fundamentals, we reexamine the transmission line and parallel-plate test problems in §4.3 and §4.4. Here, DWN structures that numerically integrate these systems are built ``the hard way'' (i.e., by association with finite difference methods and FDTD, without the benefit of a multidimensional representation), and we uncover several distinct families of such networks, in §4.3.6 and §4.4.2, with different passivity properties. We also examine the initialization of these networks in §4.5, and the implementation of boundary conditions in §4.3.9 and §4.4.4.
The next part of Chapter 4, from §4.6 to §4.9 is of a more applied nature--here we discuss several variations on the DWN form, specifically for the transmission line and parallel-plate problems. First, we take a cursory look at some other recently proposed two- and three-dimensional DWN structures in §4.6 and §4.7, extending them to the variable-coefficient case where necessary. (The spectral analysis of these DWNs is postponed until Appendix A.) We then introduce some generalized DWNs which may be useful in ``real-world'' problems, in particular those involving irregular boundary configurations and sharp variations in material parameters. We look at DWNs in the important special case of polar coordinates in §4.6.2, and then extend the same technique to general curvilinear coordinate systems in §4.8. Another means of tackling such irregularities, with an eye towards computational efficiency considerations, involves the use of multigrid DWNs; a ``fine'' DWN can be used over any part of the problem domain where greater detail is required, and may be interfaced to a ``coarse'' DWN operating over the remainder of the domain. The interface between such DWNs can be designed so as to maintain perfect losslessness, while introducing minimal numerical reflection. We look at several types of such layers, in two and three spatial dimensions, as well as a way of interfacing grids in different coordinate systems, in §4.9. Several simulations are presented, in §4.6.2, §4.9.1, and §4.9.4.
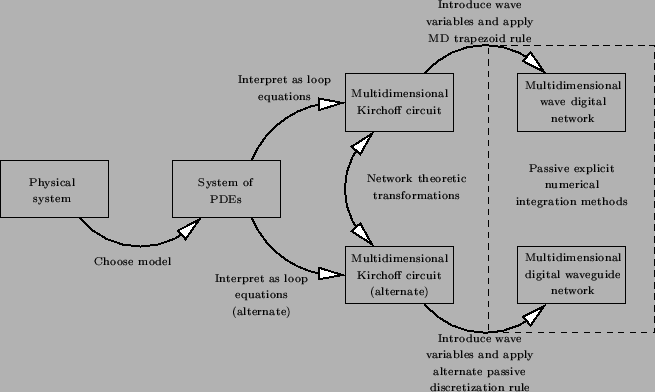
Up until this point in Chapter 4, we treat digital waveguide networks as large collections of scattering junctions connected by paired delay lines, just like the Kelly-Lochbaum model of §1.1.1 and the mesh of §1.1.2. While this is a useful vantage point, especially when it comes to constructing irregular networks such as those discussed in §4.9, and for finding proper passive boundary terminations, it is somewhat lacking in that it does not allow the algorithm designer any guidance in the construction of these methods for more complex systems. Indeed, when faced with a many-variable system (such as, for example, the thirteen-variable system of PDEs which models vibration in a stiff cylindrical shell, to be discussed in §5.5.2), it becomes difficult to proceed as was done for the comparatively simple transmission line test problems in §4.3 and §4.4. A MDWD-based method does not fall prey to these design difficulties because it follows directly from a multidimensional circuit representation of a given defining system of PDEs; in other words, a passive numerical method can be automatically generated from the model system, regardless of its complexity. It is true, however, that this circuit representation is highly non-unique--we have all of classical network theory at our disposal in order to manipulate it. What is more, while WDF discretization is based on the use of the trapezoid rule (or bilinear transform), in multiple dimensions, the family of passive integration rules is much more general. The most important result in this thesis is presented in §4.10; we use the flexibilities mentioned above in order to show that a DWN also can be viewed as the discrete image of an MDKC. As such, it can be directly incorporated into the same family as the WDF-based methods; the relationship is shown in Figure 1.14. The range of physical systems to which the DWN can be applied as a simulation method is thus considerably enlarged to include any system that has been dealt with using MDWDFs. MDWDFs and DWNs are now on an equal footing, (and we will emphasize the fraternal relationship between the two methods repeatedly in Chapter 5). We develop alternative network representations suitable for DWN discretization for the transmission line and parallel-plate systems in §4.10.3 and §4.10.4, then continue our previously postponed treatment of higher-order spatially accurate DWNs in §4.10.5, and finally conclude with a DWN for Maxwell's Equations in §4.10.6. The DWN for this last system, in that it is equivalent to Yee's original FDTD formulation completes the circle of ideas begun in the first part of the chapter.

|