This paper collects together various facts about
digital waveguide
networks (DWN) used in acoustic modeling, particularly results
pertaining to
lossless scattering at the junction of
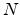
intersecting
digital waveguides. Applications discussed include music synthesis
based on physical models and
delay effects such as
artificial
reverberation. Connections with
Wave Digital Filters (WDF),
ladder/lattice
digital filters, and other related topics are outlined.
General conditions for losslessness and passivity are specified.
Computational complexity and
dynamic range requirements are addressed.
Both physical and algebraic analyses are utilized. The physical
interpretation leads to many of the desirable properties of DWNs.
Using both physical and algebraic approaches, three new normalized
ladder filter structures are derived which have only three
multiplications per two-port
scattering junction instead of the four
required in the well known version. A vector
scattering formulation
is derived which maximizes generality subject to maintaining desirable
properties. Scattering junctions are generalized to allow any
waveguide to have a complex
wave impedance which is equivalent at
the junction to a lumped load
impedance, thus providing a convenient
bridge between lumped and
distributed modeling methods. Junctions
involving complex wave impedances yield generalized scattering
coefficients which are frequency dependent and therefore implemented
in practice using digital
filters.
Scattering filters are typically
isolable to one per junction in a manner analogous to the multiply in
a one-multiply
lattice-filter section.