Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
First we address the scalar case. For an ideal acoustic tube, we have the
following wave equation [60]:
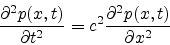 |
(1) |
where 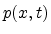 denotes (scalar) pressure in the tube at the point
denotes (scalar) pressure in the tube at the point 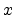 along the tube at time
along the tube at time 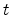 in seconds. If the length of the tube is
in seconds. If the length of the tube is
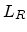 , then
, then 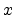 is taken to lie between
is taken to lie between 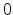 and
and 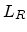 . We adopt the
convention that
. We adopt the
convention that 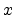 increases ``to the right'' so that waves traveling
in the direction of increasing
increases ``to the right'' so that waves traveling
in the direction of increasing 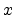 are referred to as ``right-going.''
The constant
are referred to as ``right-going.''
The constant 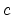 is the speed of sound propagation in the tube, given
by
is the speed of sound propagation in the tube, given
by
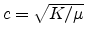 , where
, where 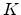 is the
``spring constant'' or ``stiffness'' of the air in the
tube,2 and
is the
``spring constant'' or ``stiffness'' of the air in the
tube,2 and 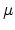 is
the mass per unit volume of the tube. The dual variable, volume velocity
is
the mass per unit volume of the tube. The dual variable, volume velocity
 , also obeys (1) with
, also obeys (1) with 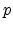 replaced by
replaced by  . The wave equation
(1) also holds for an ideal string, if
. The wave equation
(1) also holds for an ideal string, if 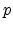 represents the transverse
displacement,
represents the transverse
displacement, 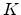 is the tension of the string, and
is the tension of the string, and 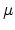 is its linear mass density.
is its linear mass density.
The wave equation (1) follows from the more physically meaningful
telegrapher's equations [24]:
Equation (2) follows immediately from Newton's second law of motion, while (3) follows
from conservation of mass and properties of an ideal gas [61].
The general traveling-wave solution to (1), (2), and (3)
was given by D'Alembert [60] as
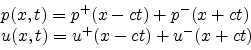 |
(4) |
where
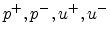 are
the right- and left-going wave components of pressure and velocity,
respectively, and are referred to as wave variables.
This solution form is interpreted as the sum of two
fixed wave-shapes traveling in opposite directions along the uniform tube. The
specific waveshapes are determined by the initial pressure
are
the right- and left-going wave components of pressure and velocity,
respectively, and are referred to as wave variables.
This solution form is interpreted as the sum of two
fixed wave-shapes traveling in opposite directions along the uniform tube. The
specific waveshapes are determined by the initial pressure 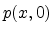 and velocity
and velocity 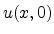 throughout the tube for
throughout the tube for ![$x\in [0,L_R]$](img38.png) .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download wgj.pdf