Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
We consider first diagonal impedance matrices, since they have
an intuitive physical counterpart in lossless acoustic tubes. Under this assumption,
we have the impedance matrix
![\begin{displaymath}
{\mbox{\boldmath$R$}}=\hbox{diag}[R_1,\dots,R_n]
\end{displaymath}](img189.png) |
(28) |
and the admittance matrix
![\begin{displaymath}
{\mbox{\boldmath$\Gamma$}}=\hbox{diag}[\Gamma_1,\dots,\Gamma_n] = {\mbox{\boldmath$R$}}^{-1}.
\end{displaymath}](img190.png) |
(29) |
By (19) and the assumption of a passive medium,
the normalized pressure waves are uniquely defined as
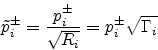 |
(30) |
where the three signs above are all taken as `` '' or all as ``
'' or all as ``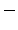 ''.
(Square roots in this paper are always taken as positive.) We can write
also
''.
(Square roots in this paper are always taken as positive.) We can write
also
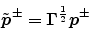 |
(31) |
where
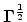 is the diagonal square root of
is the diagonal square root of
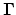 .
The junction of normalized waveguides is in this case represented by the
scattering matrix
.
The junction of normalized waveguides is in this case represented by the
scattering matrix
 |
(32) |
As a side note, this equation is analogous to the relation between
power-wave scattering matrices and voltage-wave scattering matrices as
found in the WDF literature [27] for lumped circuit elements.
In the more general case, when the (complex) admittance
matrix 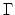 is not necessarily diagonal, but remains positive
semidefinite as required for lossless propagation, we have that
is not necessarily diagonal, but remains positive
semidefinite as required for lossless propagation, we have that
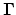 admits a Cholesky factorization
admits a Cholesky factorization
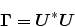 |
(33) |
where
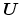 is upper triangular. We can define the normalized pressure
waves as
is upper triangular. We can define the normalized pressure
waves as
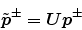 |
(34) |
The normalized scattering junction is obtained via the following
similarity transformation on the unnormalized scattering matrix:
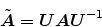 |
(35) |
Theorem 1
The scattering matrix of a normalized junction is unitary, i.e.,
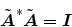 |
(36) |
Proof:
From the condition of losslessness (26), we have
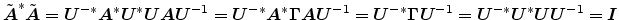
By an explicit computation of the matrix product in
(36) we can show that the terms of any column of
 are power complementary, i.e.,
are power complementary, i.e.,
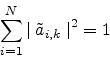 |
(37) |
for all 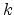 .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download wgj.pdf
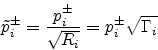
![]() is not necessarily diagonal, but remains positive
semidefinite as required for lossless propagation, we have that
is not necessarily diagonal, but remains positive
semidefinite as required for lossless propagation, we have that
![]() admits a Cholesky factorization
admits a Cholesky factorization
![]() are power complementary, i.e.,
are power complementary, i.e.,