Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The Lossless Junction
A scattering junction of waveguide sections is characterized by its
scattering matrix
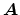 . The relationship between the
. The relationship between the 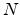 incoming
and outgoing traveling waves is given by:
incoming
and outgoing traveling waves is given by:
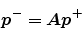 |
(23) |
where
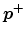 is the vector of incoming waves (assumed scalar here) and
is the vector of incoming waves (assumed scalar here) and
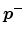 is the vector
of outgoing waves relative to the junction (see
Fig. 2). We say that the junction is
is the vector
of outgoing waves relative to the junction (see
Fig. 2). We say that the junction is 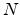 -way (or
it has
-way (or
it has 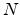 branches) if
branches) if 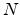 is the dimension of the incoming and
outgoing wave vectors.
is the dimension of the incoming and
outgoing wave vectors.
Figure:
A schematic depiction of the 3-way waveguide junction.
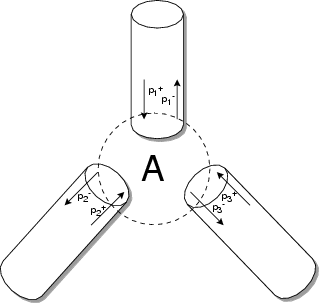 |
We now consider the case of a constant scattering matrix
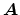 . The
more general case of scattering matrices as functions of
. The
more general case of scattering matrices as functions of  will be
considered in Section 10.
will be
considered in Section 10.
The net complex power entering the junctions is
where
 is the diagonal matrix containing the
is the diagonal matrix containing the 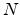 wave admittances of all
the branches meeting at the junction. Assuming the branch admittances are
Hermitian and nonzero,
we have that
wave admittances of all
the branches meeting at the junction. Assuming the branch admittances are
Hermitian and nonzero,
we have that
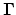 has positive real elements along its diagonal and zeros elsewhere.
The quantity
has positive real elements along its diagonal and zeros elsewhere.
The quantity
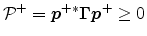 is incoming active
power, and
is incoming active
power, and
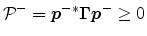 is then the outgoing active
power relative to the junction. The term
is then the outgoing active
power relative to the junction. The term
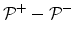 is the absorbed
active power, while the term
is the absorbed
active power, while the term
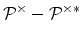 , containing
the mixed incoming and outgoing waves, is called the reactive power.
, containing
the mixed incoming and outgoing waves, is called the reactive power.
A scattering junction is said to be passive when
the absorbed active power is nonnegative, i.e., when
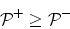 |
(25) |
for 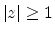 . In other terms, the outgoing active power does not
exceed the incoming active power.
. In other terms, the outgoing active power does not
exceed the incoming active power.
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download wgj.pdf
![]() . The relationship between the
. The relationship between the ![]() incoming
and outgoing traveling waves is given by:
incoming
and outgoing traveling waves is given by:
![]() . The
more general case of scattering matrices as functions of
. The
more general case of scattering matrices as functions of ![]() will be
considered in Section 10.
will be
considered in Section 10.