Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The formulation of sections 3 and 4 can be
restated for the more general case in which the scattering matrix
has elements which are functions of 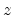 .
.
In this case the scattering relationship is
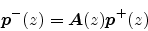 |
(86) |
In the case of lossless propagation, the scattering junction is said
to be lossless if
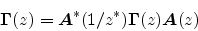 |
(87) |
In the more general case of passive propagation, the scattering junction is
said to be lossless if
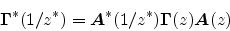 |
(88) |
By adding (89) to its conjugate transpose we get
![\begin{displaymath}
{\mbox{\boldmath$\Gamma$}}(z) + {\mbox{\boldmath$\Gamma$}}^...
...+ {\mbox{\boldmath$\Gamma$}}^*(1/z^*)]{\mbox{\boldmath$A$}}(z)
\end{displaymath}](img474.png) |
(89) |
and we see that
the construction of a normalized scattering matrix proceeds from a
spectral factorization (if it exists) of the real part of the
admittance matrix:
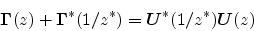 |
(90) |
When the medium is passive we have
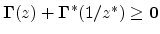 , and a spectral factorization does exist. The normalized
scattering matrix is then
, and a spectral factorization does exist. The normalized
scattering matrix is then
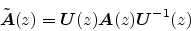 |
(91) |
and it is para-unitary, i.e.,
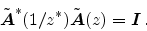 |
(92) |
A real-coefficient matrix
 which is analytic for
which is analytic for 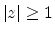 and which satisfies (93) is called Lossless Bounded
Real [63,112]. The condition (93) implies
that the elements of any column of
and which satisfies (93) is called Lossless Bounded
Real [63,112]. The condition (93) implies
that the elements of any column of
 are power complementary,
i.e.,
are power complementary,
i.e.,
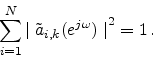 |
(93) |
In fixed-point implementations, the condition (94) can be
satisfied as shown in [71,83,114]. Given a set of
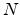 power-complementary filters {
power-complementary filters {
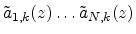 }, they can be implemented by means of
}, they can be implemented by means of 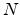 allpass
filters under mild conditions [114], and the property of power
complementarity is structurally induced in the sense that coefficient
quantization cannot alter it.
allpass
filters under mild conditions [114], and the property of power
complementarity is structurally induced in the sense that coefficient
quantization cannot alter it.
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download wgj.pdf
![]() .
.
![]() which is analytic for
which is analytic for ![]() and which satisfies (93) is called Lossless Bounded
Real [63,112]. The condition (93) implies
that the elements of any column of
and which satisfies (93) is called Lossless Bounded
Real [63,112]. The condition (93) implies
that the elements of any column of
![]() are power complementary,
i.e.,
are power complementary,
i.e.,