- ... Arrays1
- Published 2019-11-18:
http://arxiv.org/abs/1911.07575
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... point.2
- A nice overview of ambisonics
references appears on the
Web:
http://www.york.ac.uk/inst/mustech/3d_audio/gerzonrf.htm
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...BerkhoutEtAl93,3
- https://en.wikipedia.org/wiki/Wave_field_synthesis
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... avoided.4
- Ambisonics can also
approach physical completeness of the soundfield, as the order (number
of spherical harmonics) increases, but most practical systems are
fairly low order. (The highest order used at CCRMA is presently
seven.) First-order ambisonics is essentially stereo (representable
as a monopole plus one left-right dipole) augmented to include
front-back and top-down dipoles.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(1690).5
- https://www.britannica.com/science/Huygens-principle
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... approximation;6
- Since every
source-free soundfield can be constructed as a superposition of
plane waves, it follows that solving the plane-wave synthesis
problem is quite general.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sphere''.7
- This analogy for PBAP sources as point-sources
(stars) on the celestial sphere motivates the alternate name ``Star
Field Synthesis (SFS).'' Viewing a starfield through a window is a
vivid analogy for PBAP using a rectangular speaker array. However,
diffraction effects are much more significant in SFS (especially at
low frequencies) than when viewing light through a rectangular
aperture, so the analogy can be misleading.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...band-limited8
- https://ccrma.stanford.edu/~jos/resample/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...PASP.9
- https://ccrma.stanford.edu/~jos/pasp/Delay_Line_Signal_Interpolation.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
center-front.10
- http://acousticslab.org/psychoacoustics/PMFiles/Module07a.htm
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...PASP.11
- https://ccrma.stanford.edu/~jos/pasp/Software_Delay_Line.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... direction.12
- The analogous condition for Wave Field
Synthesis is to use only secondary sources that are ``illuminated'' by
the virtual source being rendered (Ahrens, 2012).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... perception.13
- http://en.wikipedia.org/wiki/Head-related_transfer_function
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...14
- http://en.wikipedia.org/wiki/Sound_localization#ITD_and_ILD.
In (Gerzon, 1974), citing
Rayleigh from 1907, the low-frequency crossover is given as 700
Hz. It is also noted in (Gerzon, 1974) that pinnae filtering is
thought to be important above 5 kHz.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...SASP.15
- https://ccrma.stanford.edu/~jos/sasp/Spectrum_Analysis_Windows.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
error.16
- https://ccrma.stanford.edu/~jos/sasp/Window_Design_Linear_Programming.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Wierstorf2012a.17
- https://github.com/sfstoolbox/sfs
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... excursion.18
- To
see this, consider that the speaker is much smaller than the
wavelength produced at its low end, so it can be regarded as an
approximate ``point source'' in that frequency range. From the theory
of a point source (Morse and Ingard, 1968, p. 310), the peak pressure-amplitude from
a sinusoidally oscillating point source is proportional to the
peak volume acceleration from the source, which is in turn
proportional to the radial acceleration (second time-derivative
of spherical radius) for any small sphere used to model the simple
source. (Any sphere much smaller than a
wavelength in diameter will do.) Let the spherical radius acceleration
be denoted
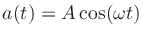 , which is proportional to the
far-field pressure a fixed distance away. Then the peak radial
excursion of the spherical surface is given by
, which is proportional to the
far-field pressure a fixed distance away. Then the peak radial
excursion of the spherical surface is given by
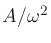 , and
keeping the excursion fixed while decreasing
, and
keeping the excursion fixed while decreasing 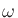 by one octave
reduces the far-field pressure by a factor of four, or
by one octave
reduces the far-field pressure by a factor of four, or 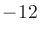 dB. When
operating as a cell of a planar array, on the other hand, far-field
pressure is proportional to the driver surface velocity instead
of acceleration. In that case, only 6 dB per octave is lost
integrating velocity to get displacement.
dB. When
operating as a cell of a planar array, on the other hand, far-field
pressure is proportional to the driver surface velocity instead
of acceleration. In that case, only 6 dB per octave is lost
integrating velocity to get displacement.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
purpose.19
- https://ccrma.stanford.edu/~jos/pasp/Vector_Wavenumber.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
reconstruction.20
- The 2D Fourier transform of
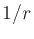 can be
shown to be
can be
shown to be
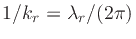 :
:
http://sepwww.stanford.edu/public/docs/sep103/jon3/paper_html/node3.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... above.21
- This spectral partition issue is related
to the classic ``panning problem'' in which low frequencies see a 3dB
boost relative to high frequencies, due to coherent versus noncoherent
summation from stereo speakers for an off-axis
listener: https://ccrma.stanford.edu/~jos/sasp/Panning_Problem.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....22
-
https://adriftjustoffthecoast.wordpress.com/2013/06/06/2d-fourier-transform-of-the-unit-disk/,
http://www.robots.ox.ac.uk/~az/lectures/ia/lect2.pdf
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
four-way:23
- https://www.acs.psu.edu/drussell/Demos/BaffledPiston/BaffledPiston.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
cm.24
- These are ``octave spaced'' from midrange to
super-tweeter, with an extra large woofer. To adhere to octave
spacing, the woofer diameter could be changed to 24 cm and the lower
frequencies could be taken over by a subwoofer where the woofer
leaves off.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
radius.25
- This implies the lower speaker diameter is 1.75
wavelengths at crossover while the upper speaker diameter is 0.7
(midrange) or 0.88 (tweeter and super-tweeter) wavelengths at
crossover. The geometric means of these two diameters in wavelengths
are 1.1 (woofer-midrange) and 1.24 (other two crossovers)
wavelengths. The general tradeoff is that driving with diameter
less than a wavelength is inefficient (below cutoff), but yields
nicely omnidirectional radiation, while driving with diameter much
larger than a wavelength becomes highly directional.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... divisions.26
- We avoid the term
``Huygens Octave Array'' (HOA), which would be nice to use for
planar arrays as in Fig.9, due to the common use of HOA
as ``Higher Order Ambisonics''. It is convenient to organize
multiresolution line arrays into panels, so not much is lost.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... etc.27
- 2019-09-30: https://en.wikipedia.org/wiki/Subwoofer
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
field.28
- http://acousticslab.org/psychoacoustics/PMFiles/Module07a.htm
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... away.29
- A great demonstration of this effect in
stereo, is to turn on a gated sinusoid in, say, the right speaker,
cross-fade the signal over to the left speaker, then pull out the
right speaker cable and hand it to the befuddled listener who still
hears the tone coming out of the right speaker. Thanks to Bill
Putnam for showing me this one.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... system.30
- https://www.svsound.com/blogs/svs/strengths-and-pitfalls-of-big-subwoofer-drivers
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
listeners,31
- See International Standard ISO-7029:2017 (3rd
edition): https://www.iso.org/standard/42916.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zone.''32
- A single-frequency soundfield is always highly
correlated at distances less than a quarter wavelength or so, even
when it is randomly constructed as a sum of plane waves from all
directions with random phases (a ``diffuse field''
(Smith, 2010; Pierce, 1989; Beranek, 1986)). Even in a richly reverberant
environment, one can imagine ``correlation bubbles'' on the order of
the wavelength at each frequency.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... documentation.33
- https://sfs.readthedocs.io/en/3.2/problem/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formulas.34
- For
a definition of ``frequency response'' and related terms,
see, e.g., (Smith, 2007a).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
circle.35
- Matlab for these figures is available
at
https://ccrma.stanford.edu/~jos/huygens/matlab.tgz
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.