We have so far considered only PBAP and its variants, which can be considered Far-Field Wave Field Synthesis (FFWFS), in which each source contributes a plane wave to each listening point. This is pretty general, in principle, because, as is well known, every source-free soundfield can be expressed as a sum of plane waves at various amplitudes, phases, and directions of arrival. In fact, Fourier transform methods can be used for this purpose.19Therefore, a straightforward path from FFWFS to full-fledged WFS is to decompose any desired soundfield into a sum of plane waves, and then generate those plane waves using FFWFS/PBAP. There are many known methods for so-called Plane-wave Decomposition (PWD) (Pulkki, 2017).
A more direct extension of PBAP toward WFS is based again on simple sampling of the acoustic source wave, but now allowing spherical waves instead of only plane waves in the soundfield reconstruction. We could call this Sphere-Based Range and Angle Panning (SBRAP). However, reconstructing a wavefront as a superposition of spherical waves is essentially the idea of Huygens' Principle. We therefore choose the name Huygens Array (HA) for the extension of PBAP to include spherical as well as planar wavefronts.
For constructing a Huygens Array, each virtual source
![]() is at a known
location in 3D space:
is at a known
location in 3D space:
According to the basic sampling assumption in PBAP, each speaker location is also a microphone location, so we can denote the
In PBAP, each virtual source
![]() was characterized by an angle of arrival
was characterized by an angle of arrival
![]() , which determined the inter-speaker delay
, which determined the inter-speaker delay
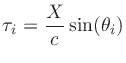
in seconds along the line array, where
Let ![]() denote the amplitude of source
denote the amplitude of source ![]() at a distance one meter
from its center. (Each source is assumed to be a point source for
now; distributed sources can be modeled as weighted sums of point
sources.) Then for the delays we have
at a distance one meter
from its center. (Each source is assumed to be a point source for
now; distributed sources can be modeled as weighted sums of point
sources.) Then for the delays we have
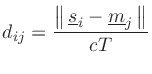
where
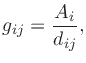
and, if desired, lowpass-filtering due to air absorption can be included:
where
http://arxiv.org/abs/1911.07575.