Since high-quality fractional-delay filtering is expensive, it is
worth considering restriction to angles-of-arrival corresponding to
integer delays (in samples). If the speaker-to-speaker spacing
along a line array is ![]() ,
then the speaker-to-speaker delay for a plane wave at
angle-of-incidence
,
then the speaker-to-speaker delay for a plane wave at
angle-of-incidence ![]() is
is
![]() , where
, where ![]() denotes sound speed. Thus, an angle-of-arrival
denotes sound speed. Thus, an angle-of-arrival ![]() corresponds
to an integer speaker-to-speaker delay
corresponds
to an integer speaker-to-speaker delay ![]() (in samples) when
(in samples) when
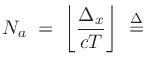 floor
floor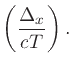
Note that increasing the speaker spacing
It is clearly inaudible to shift the location of each virtual source
![]() so that the time delay to the nearest speaker is an integer
number of samples. Then having an integer number of samples for each
inter-speaker delay makes all the delays integer. Finally, this can
all be implemented as a single delay line with a tap
(non-interpolating) for each speaker signal. For moving sources, to
avoid clicks, moving taps should be cross-faded from one integer delay
to the next in the usual way (Smith, 2010).9
so that the time delay to the nearest speaker is an integer
number of samples. Then having an integer number of samples for each
inter-speaker delay makes all the delays integer. Finally, this can
all be implemented as a single delay line with a tap
(non-interpolating) for each speaker signal. For moving sources, to
avoid clicks, moving taps should be cross-faded from one integer delay
to the next in the usual way (Smith, 2010).9
Solving Eq.(5), the collection of angles ![]() corresponding to integer inter-speaker delays
corresponding to integer inter-speaker delays ![]() (in samples) is
(in samples) is
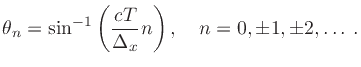 |
(6) |
Figure 4 depicts the available geometric rays of plane-wave
propagation for this example. Thicker rays are drawn for 0 degrees
(directly in front) and ![]() degrees (full left and right).
degrees (full left and right).
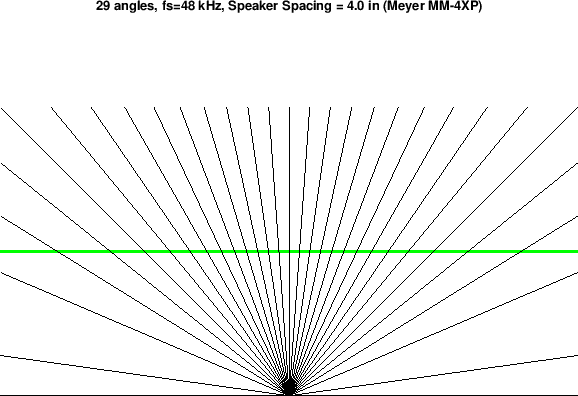
|
If the 21 angles-of-arrival across a ![]() stage listed in
Eq.(7) are deemed sufficient, then PBAP is essentially free:
just provide the appropriate integer adjacent-speaker delays for each
source in the sum for each speaker. As is well known, an integer
delay is an
stage listed in
Eq.(7) are deemed sufficient, then PBAP is essentially free:
just provide the appropriate integer adjacent-speaker delays for each
source in the sum for each speaker. As is well known, an integer
delay is an
![]() computation, requiring only a single read,
write, and circular-buffer pointer-increment each sampling instant
(Smith, 2010).11
computation, requiring only a single read,
write, and circular-buffer pointer-increment each sampling instant
(Smith, 2010).11
http://arxiv.org/abs/1911.07575.