The delay line is an elementary functional unit which models acoustic propagation delay. It is a fundamental building block of both delay-effects processors and digital-waveguide synthesis models. The function of a delay line is to introduce a time delay between its input and output, as shown in Fig.2.1.
Let the input signal be denoted
![]() , and let the
delay-line length be
, and let the
delay-line length be ![]() samples. Then the output signal
samples. Then the output signal ![]() is
specified by the relation
is
specified by the relation
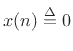 for
for
Before the digital era, delay lines were expensive and imprecise in
``analog'' form. For example, ``spring reverberators'' (common in
guitar amplifiers) use metal springs as analog delay lines; while
adequate for that purpose, they are highly dispersive and prone to
noise pick-up. Large delays require prohibitively long springs or
coils in analog implementations. In the digital domain, on the other
hand, delay by ![]() samples is trivially implemented, and non-integer
delays can be implemented using interpolation techniques, as discussed
later in §4.1.
samples is trivially implemented, and non-integer
delays can be implemented using interpolation techniques, as discussed
later in §4.1.