Overview of Planewave-Based Angle Panning (PBAP)

Figure 1: Assumed geometry of primary sources, mic- or speaker-array (or secondary sources), and listening space in PBAP. The primary sources and mic-array are separated by many wavelengths so that the microphones only need to record pressure samples of a superposition of plane waves. The speaker-array is then designed to try to reproduce this superposition of plane waves from its samples along the array.

Studying Wave Field Synthesis (WFS) led to the idea of the considerably simpler Planewave-Based Angle Panning (PBAP), which could just as well be called Far-Field Wave Field Synthesis (FFWFS). The simplifying assumptions of PBAP are

1. the microphone-array is positioned between the primary sources and the listeners, e.g., between a ``stage'' and all the ``seats'' in an auditorium, for example, as shown in Fig.1;

2. the microphone-array is at least several wavelengths away from the nearest source, so that the mic-array sees a superposition of plane waves to a good approximation;⁶ and

3. the speaker-array lies along a line parallel to or coincident with the mic array in the direction of the audience.

The simplest case of assumption 3 is when the speakers and microphones are coincident, i.e., $N=M$ and the speaker array lies along the same line as the mic array, so that each speaker reproduces the signal recorded at its microphone. The mic array can be viewed as a spatial A/D converter, sampling the incident wavefront, and the coincident speaker array gives the corresponding spatial D/A converter for these microphone samples. When $N\ne M$ or when not coincident and not spaced in a compensating manner, we must compute the speaker signals from spatial-resampling of the mic signals.

The main point is that PBAP is obtained from WFS by moving all acoustic sources to ``infinity''--i.e., onto the ``celestial sphere''.⁷ In practical acoustics, ``infinity'' means ``many wavelengths,'' and thus depends on frequency. Huygens Arrays, developed next, generalize the linear/planar sampling arrays to more geometries while keeping a separation plane between primary sources and listeners.

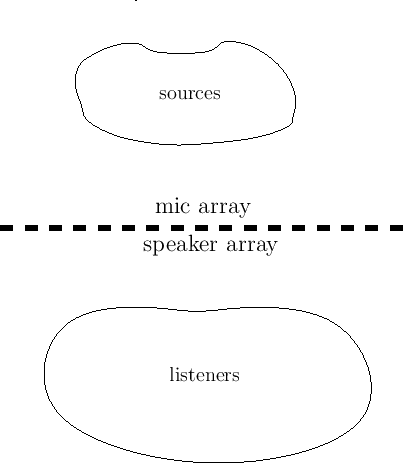
Figure 1 illustrates the basic geometry assumed for single-line-array PBAP. All sources are confined to a ``stage area,'' which can be a 3D distribution of sources when the microphone-array is planar, but such a distribution is effectively 2D due to assumption 2 (the microphones are in the ``far field'' of each source). All listeners are confined to the ``audience area'' which can also be a 3D distribution of ``seats,'' when the speaker-array is planar, but again the far-field assumption implies that each seat hears substantially the same planar distribution of sources far away. The microphone- and speaker-arrays thus form a separation plane between the stage and audience areas. For the line-array case, the sources are considered as being arranged on a flat stage (same height--only azimuth varying--the same case addressed by ordinary stereo).

In summary, our assumptions allow us to reconstruct a superposition of plane waves given pressure samples along any plane separating the source and audience area. Since the microphone-array is our pressure-sampling array, it is natural to choose uniform spacing of the microphones along each coordinate dimension. (It is reasonable to choose a smaller spacing for the horizontal direction since people are more sensitive to azimuth than to elevation of source angle-of-arrival.) Furthermore, we need to ensure that the incident wavefield is properly band-limited⁸ (Smith, 2010). In normal signal sampling, an anti-aliasing lowpass-filter removes high-frequency components that would alias. In the spatial sampling array, we can simply require that the incoming plane waves have a known maximum angle that does not ``alias'' spatially. This limits the angular ``stage width.''