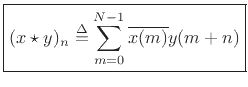Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Correlation
The correlation operator for two signals 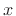 and
and  in
in
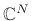 is defined as
is defined as
We may interpret the correlation operator as
which is proportional to
the coefficient of projection of  onto
onto 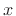 advanced by
advanced by
 samples (shifted circularly to the left by
samples (shifted circularly to the left by  samples). The
time shift
samples). The
time shift  is called the correlation lag, and
is called the correlation lag, and
 is called a lagged product. Applications of correlation
are discussed in §8.4.
is called a lagged product. Applications of correlation
are discussed in §8.4.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() and
and ![]() in
in
![]() is defined as
is defined as