The orthogonal projection (or simply ``projection'') of
![]() onto
onto
![]() is defined by
is defined by
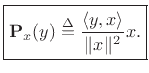
The complex scalar
Motivation: The basic idea of orthogonal projection of ![]() onto
onto
![]() is to ``drop a perpendicular'' from
is to ``drop a perpendicular'' from ![]() onto
onto ![]() to define a new
vector along
to define a new
vector along ![]() which we call the ``projection'' of
which we call the ``projection'' of ![]() onto
onto ![]() .
This is illustrated for
.
This is illustrated for ![]() in Fig.5.9 for
in Fig.5.9 for ![]() and
and
![]() , in which case
, in which case
![$\displaystyle {\bf P}_{x}(y) \isdef \frac{\left<y,x\right>}{\Vert x\Vert^2} x
= \frac{(2\cdot \overline{4} + 3\cdot \overline{1})}{4^2+1^2} x
= \frac{11}{17} x= \left[\frac{44}{17},\frac{11}{17}\right].
$](img873.png)
Derivation: (1) Since any projection onto ![]() must lie along the
line collinear with
must lie along the
line collinear with ![]() , write the projection as
, write the projection as
![]() . (2) Since by definition the projection error
. (2) Since by definition the projection error
![]() is orthogonal to
is orthogonal to ![]() , we must have
, we must have
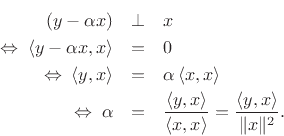
Thus,
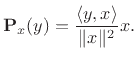
See §I.3.3 for illustration of orthogonal projection in matlab.